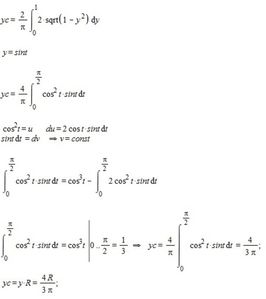Задание
Развернуть задание
Определите положение центра масс половины круглого диска радиусом R, считая его однородным.
Развернуть задание
Новое решение
Решение
Y2+X2=R2
перепишем:
Y2/R2+X2/R2 = 1
Заменим у =Y/R, x = X/R и получим:
y2+x2 = 1 - тригонометрическая окружность.
Горизонтальный элемент площади на расстоянии y от начала координат:
ds(y) = 2*x*dy= 2 Sqrt(1 - y^2) dy
Тогда
перепишем:
Y2/R2+X2/R2 = 1
Заменим у =Y/R, x = X/R и получим:
y2+x2 = 1 - тригонометрическая окружность.
Горизонтальный элемент площади на расстоянии y от начала координат:
ds(y) = 2*x*dy= 2 Sqrt(1 - y^2) dy
Тогда
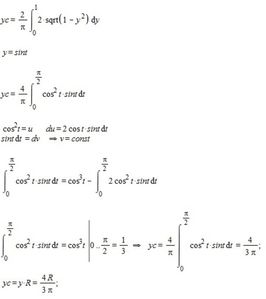
Y2+X2=R2
перепишем:
Y2/R2+X2/R2 = 1
Заменим у =Y/R, x = X/R и получим:
y2+x2 = 1 - тригонометрическая окружность.
Горизонтальный элемент площади на расстоянии y от начала координат:
ds(y) = 2*x*dy= 2 Sqrt(1 - y^2) dy
Тогда
перепишем:
Y2/R2+X2/R2 = 1
Заменим у =Y/R, x = X/R и получим:
y2+x2 = 1 - тригонометрическая окружность.
Горизонтальный элемент площади на расстоянии y от начала координат:
ds(y) = 2*x*dy= 2 Sqrt(1 - y^2) dy
Тогда