Задание
Развернуть задание
Периметр правильного треугольника, вписанного в окружность, равен 18 см. Найдите сторону квадрата, вписанного в ту же окружность.
Развернуть задание
Новое решение
Решение
Дано: ∆ABC, AB=BC=AC; FKNE – вписанный квадрат; P(ABC) = 18 см.
Найти: FK.
Так как ∆ABC – равносторонний, то AB = 18/3 = 6 см
R = OB = AB/√3 = 6/√3 = 2√3 см
Так как FKNE – вписанный квадрат, то FK = R√2.
FK = 2√3 * √2 = 2√6
Найти: FK.
Так как ∆ABC – равносторонний, то AB = 18/3 = 6 см
R = OB = AB/√3 = 6/√3 = 2√3 см
Так как FKNE – вписанный квадрат, то FK = R√2.
FK = 2√3 * √2 = 2√6
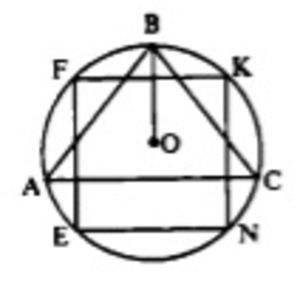
Дано: ∆ABC, AB=BC=AC; FKNE – вписанный квадрат; P(ABC) = 18 см.
Найти: FK.
Так как ∆ABC – равносторонний, то AB = 18/3 = 6 см
R = OB = AB/√3 = 6/√3 = 2√3 см
Так как FKNE – вписанный квадрат, то FK = R√2.
FK = 2√3 * √2 = 2√6
Найти: FK.
Так как ∆ABC – равносторонний, то AB = 18/3 = 6 см
R = OB = AB/√3 = 6/√3 = 2√3 см
Так как FKNE – вписанный квадрат, то FK = R√2.
FK = 2√3 * √2 = 2√6
