Задание
Развернуть задание
Около правильного треугольника описана окружность радиуса R. Докажите, что R = 2r, где r – радиус окружности, вписанной в этот треугольник.
Развернуть задание
Новое решение
Решение
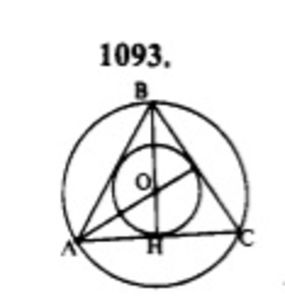
Дано: ∆ABC – правильный, Окр (0; R) – описанная, Окр (0; r) – вписанная.
Доказать, что R = 2r
Так как ∆ABC – правильный, то центры вписанной и описанной окружностей совпадают. O
– точка пересечения биссектрис, которые в равностороннем треугольнике являются
медианами.
По свойству медиан: BO/OH = 2/1, а т.к. BO = R, OH = r, то
R/r = 2/1 => R = 2r
Доказать, что R = 2r
Так как ∆ABC – правильный, то центры вписанной и описанной окружностей совпадают. O
– точка пересечения биссектрис, которые в равностороннем треугольнике являются
медианами.
По свойству медиан: BO/OH = 2/1, а т.к. BO = R, OH = r, то
R/r = 2/1 => R = 2r
Дано: ∆ABC – правильный, Окр (0; R) – описанная, Окр (0; r) – вписанная.
Доказать, что R = 2r
Так как ∆ABC – правильный, то центры вписанной и описанной окружностей совпадают. O
– точка пересечения биссектрис, которые в равностороннем треугольнике являются
медианами.
По свойству медиан: BO/OH = 2/1, а т.к. BO = R, OH = r, то
R/r = 2/1 => R = 2r
Доказать, что R = 2r
Так как ∆ABC – правильный, то центры вписанной и описанной окружностей совпадают. O
– точка пересечения биссектрис, которые в равностороннем треугольнике являются
медианами.
По свойству медиан: BO/OH = 2/1, а т.к. BO = R, OH = r, то
R/r = 2/1 => R = 2r
