Задание
Развернуть задание
Найдите отношение площадей двух правильных шестиугольников – вписанного в окружность и описанного около нее.
Развернуть задание
Новое решение
Решение
Дано: ABCDEF – описанный правильный 6-угольник, A_1B_1C_1D_1E_1F_1 – вписанный
правильный 6-угольник.
Найти S_1 : S_2
A_1B_1C_1D_1E_1F_1 – вписанный в окружность, то A_1B_1 = B_1C_1 = … = F_1A_1 = R
S_(A_1B_1C_1D_1E_1F_1) = 6S_(∆A_1OB_1) = 6 * (1/2 * OA_1 * OB_1 * sin(60˚)) = 3 * R * R
* √3/2 = 3√(3R^2)/2
OA – биссектриса ∠A_1OF_1 => ∠A_1OA = 30˚; A_1A = x, получим OA = 2x. По теореме
Пифагора:
A_1A^2 + OA_1^2 = OA^2
x^2 + R^2 = 4x^2
3x^2 = R^2 => x = R√3/3
AB = 2R√3/3
S_(ABCDEF) = 6 * (1/2 OA * OB * sin 60˚) = 3 * (2√(3R)/3)^2 * √3/2 = 4*3*R^2 * √3/6 = 2R^2√3
S_(A_1B_1C_1D_1E_1F_1) : S_(ABCDEF) = 3√(3R^2)/2 : 2R^2√3 = 3/4
правильный 6-угольник.
Найти S_1 : S_2
A_1B_1C_1D_1E_1F_1 – вписанный в окружность, то A_1B_1 = B_1C_1 = … = F_1A_1 = R
S_(A_1B_1C_1D_1E_1F_1) = 6S_(∆A_1OB_1) = 6 * (1/2 * OA_1 * OB_1 * sin(60˚)) = 3 * R * R
* √3/2 = 3√(3R^2)/2
OA – биссектриса ∠A_1OF_1 => ∠A_1OA = 30˚; A_1A = x, получим OA = 2x. По теореме
Пифагора:
A_1A^2 + OA_1^2 = OA^2
x^2 + R^2 = 4x^2
3x^2 = R^2 => x = R√3/3
AB = 2R√3/3
S_(ABCDEF) = 6 * (1/2 OA * OB * sin 60˚) = 3 * (2√(3R)/3)^2 * √3/2 = 4*3*R^2 * √3/6 = 2R^2√3
S_(A_1B_1C_1D_1E_1F_1) : S_(ABCDEF) = 3√(3R^2)/2 : 2R^2√3 = 3/4
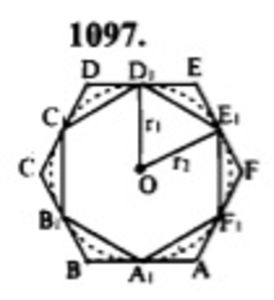
Дано: ABCDEF – описанный правильный 6-угольник, A_1B_1C_1D_1E_1F_1 – вписанный
правильный 6-угольник.
Найти S_1 : S_2
A_1B_1C_1D_1E_1F_1 – вписанный в окружность, то A_1B_1 = B_1C_1 = … = F_1A_1 = R
S_(A_1B_1C_1D_1E_1F_1) = 6S_(∆A_1OB_1) = 6 * (1/2 * OA_1 * OB_1 * sin(60˚)) = 3 * R * R
* √3/2 = 3√(3R^2)/2
OA – биссектриса ∠A_1OF_1 => ∠A_1OA = 30˚; A_1A = x, получим OA = 2x. По теореме
Пифагора:
A_1A^2 + OA_1^2 = OA^2
x^2 + R^2 = 4x^2
3x^2 = R^2 => x = R√3/3
AB = 2R√3/3
S_(ABCDEF) = 6 * (1/2 OA * OB * sin 60˚) = 3 * (2√(3R)/3)^2 * √3/2 = 4*3*R^2 * √3/6 = 2R^2√3
S_(A_1B_1C_1D_1E_1F_1) : S_(ABCDEF) = 3√(3R^2)/2 : 2R^2√3 = 3/4
правильный 6-угольник.
Найти S_1 : S_2
A_1B_1C_1D_1E_1F_1 – вписанный в окружность, то A_1B_1 = B_1C_1 = … = F_1A_1 = R
S_(A_1B_1C_1D_1E_1F_1) = 6S_(∆A_1OB_1) = 6 * (1/2 * OA_1 * OB_1 * sin(60˚)) = 3 * R * R
* √3/2 = 3√(3R^2)/2
OA – биссектриса ∠A_1OF_1 => ∠A_1OA = 30˚; A_1A = x, получим OA = 2x. По теореме
Пифагора:
A_1A^2 + OA_1^2 = OA^2
x^2 + R^2 = 4x^2
3x^2 = R^2 => x = R√3/3
AB = 2R√3/3
S_(ABCDEF) = 6 * (1/2 OA * OB * sin 60˚) = 3 * (2√(3R)/3)^2 * √3/2 = 4*3*R^2 * √3/6 = 2R^2√3
S_(A_1B_1C_1D_1E_1F_1) : S_(ABCDEF) = 3√(3R^2)/2 : 2R^2√3 = 3/4
