Задание
Развернуть задание
Площадь осевого сечения цилиндра равна S. Найдите площадь сечения цилиндра плоскостью, проходящей через середину радиуса основания перпендикулярно к этому радиусу.
Развернуть задание
Новое решение
Решение
1)Пусть ABCD осевое сечение прямоугольник. r=OA-радиус. Точка P – середина радиуса OP=r/2. AB=l - образующая.
2)MNKL- плоскость перпендикулярная радиусу, прямоугольник. S=SABCD по условию.
3)Найдем площадь прямоугольника S ABCD =AD*AB=AD*KN=2rl rl=S/2
4)Найдем площадь прямоугольника SMNKL=MN*KN=l*MN
Найдем MN=2NP т.к. △PON=△MOP(по 2м сторонам и углу между ними) и NP=PM
5)Найдем по теор. Пифагора NP=√(ON2-OP2)=√(r2-(r/2)2)=(r√3)/2. Значит MN=r√3 SMNKL= lr√3=(S√3)/2
Ответ: SMNKL=(S√3)/2
2)MNKL- плоскость перпендикулярная радиусу, прямоугольник. S=SABCD по условию.
3)Найдем площадь прямоугольника S ABCD =AD*AB=AD*KN=2rl rl=S/2
4)Найдем площадь прямоугольника SMNKL=MN*KN=l*MN
Найдем MN=2NP т.к. △PON=△MOP(по 2м сторонам и углу между ними) и NP=PM
5)Найдем по теор. Пифагора NP=√(ON2-OP2)=√(r2-(r/2)2)=(r√3)/2. Значит MN=r√3 SMNKL= lr√3=(S√3)/2
Ответ: SMNKL=(S√3)/2
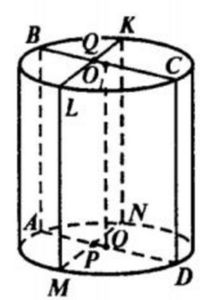
1)Пусть ABCD осевое сечение прямоугольник. r=OA-радиус. Точка P – середина радиуса OP=r/2. AB=l - образующая.
2)MNKL- плоскость перпендикулярная радиусу, прямоугольник. S=SABCD по условию.
3)Найдем площадь прямоугольника S ABCD =AD*AB=AD*KN=2rl rl=S/2
4)Найдем площадь прямоугольника SMNKL=MN*KN=l*MN
Найдем MN=2NP т.к. △PON=△MOP(по 2м сторонам и углу между ними) и NP=PM
5)Найдем по теор. Пифагора NP=√(ON2-OP2)=√(r2-(r/2)2)=(r√3)/2. Значит MN=r√3 SMNKL= lr√3=(S√3)/2
Ответ: SMNKL=(S√3)/2
2)MNKL- плоскость перпендикулярная радиусу, прямоугольник. S=SABCD по условию.
3)Найдем площадь прямоугольника S ABCD =AD*AB=AD*KN=2rl rl=S/2
4)Найдем площадь прямоугольника SMNKL=MN*KN=l*MN
Найдем MN=2NP т.к. △PON=△MOP(по 2м сторонам и углу между ними) и NP=PM
5)Найдем по теор. Пифагора NP=√(ON2-OP2)=√(r2-(r/2)2)=(r√3)/2. Значит MN=r√3 SMNKL= lr√3=(S√3)/2
Ответ: SMNKL=(S√3)/2
