Задание
Развернуть задание
Вершины A и B прямоугольника ABCD лежат на окружности одного из оснований цилиндра, а вершины C и D — на окружности другого основания. Вычислите радиус цилиндра, если его образующая равна a, AB = a, а угол между прямой BC и плоскостью основания равен 60°.
Развернуть задание
Новое решение
Решение
- Предыдущее
- Следующее
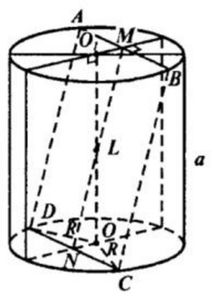
Рассмотрим основания цилиндра. Через их центры проведём диаметры, которые будут перпендикулярны сторонам AB и DC. O1M перп. АВ, ON перп. DC.
Так как диаметр, перпендикулярный хорде, делит хорду пополам, получим, что точка N – середина DC и точка M – середина АВ.
Угол NMO1 = 60* – угол между ВС и плоскостью основания. Пусть R – радиус основания цилиндра.
DC = AB = a
DN = a/2
Из ∆DNO: ON = sqrt(R^2 – a^2/4)
Из прямоугольного треугольника LON:
LO/ON = tg 60* = sqrt(3)
OL = sqrt(3)* sqrt(R^2 – a^2/4)
Рассмотрим плоскость верхнего основания:
O1M = sqrt(O1B^2 – BM^2) = (R^2 – (a/2)^2), т.е. O1M = ON
∆O1LM = ∆OLN, отсюда:
OL = O1L
O1L + LO = O1O = a
2sqrt(3) * sqrt(R^2 – a^2/4) = a
12R^2 – 3a^2 = a^2
R = a*sqrt(3)/3
Ответ: a*sqrt(3)/3
Так как диаметр, перпендикулярный хорде, делит хорду пополам, получим, что точка N – середина DC и точка M – середина АВ.
Угол NMO1 = 60* – угол между ВС и плоскостью основания. Пусть R – радиус основания цилиндра.
DC = AB = a
DN = a/2
Из ∆DNO: ON = sqrt(R^2 – a^2/4)
Из прямоугольного треугольника LON:
LO/ON = tg 60* = sqrt(3)
OL = sqrt(3)* sqrt(R^2 – a^2/4)
Рассмотрим плоскость верхнего основания:
O1M = sqrt(O1B^2 – BM^2) = (R^2 – (a/2)^2), т.е. O1M = ON
∆O1LM = ∆OLN, отсюда:
OL = O1L
O1L + LO = O1O = a
2sqrt(3) * sqrt(R^2 – a^2/4) = a
12R^2 – 3a^2 = a^2
R = a*sqrt(3)/3
Ответ: a*sqrt(3)/3

Рассмотрим основания цилиндра. Через их центры проведём диаметры, которые будут перпендикулярны сторонам AB и DC. O1M перп. АВ, ON перп. DC.
Так как диаметр, перпендикулярный хорде, делит хорду пополам, получим, что точка N – середина DC и точка M – середина АВ.
Угол NMO1 = 60* – угол между ВС и плоскостью основания. Пусть R – радиус основания цилиндра.
DC = AB = a
DN = a/2
Из ∆DNO: ON = sqrt(R^2 – a^2/4)
Из прямоугольного треугольника LON:
LO/ON = tg 60* = sqrt(3)
OL = sqrt(3)* sqrt(R^2 – a^2/4)
Рассмотрим плоскость верхнего основания:
O1M = sqrt(O1B^2 – BM^2) = (R^2 – (a/2)^2), т.е. O1M = ON
∆O1LM = ∆OLN, отсюда:
OL = O1L
O1L + LO = O1O = a
2sqrt(3) * sqrt(R^2 – a^2/4) = a
12R^2 – 3a^2 = a^2
R = a*sqrt(3)/3
Ответ: a*sqrt(3)/3
Так как диаметр, перпендикулярный хорде, делит хорду пополам, получим, что точка N – середина DC и точка M – середина АВ.
Угол NMO1 = 60* – угол между ВС и плоскостью основания. Пусть R – радиус основания цилиндра.
DC = AB = a
DN = a/2
Из ∆DNO: ON = sqrt(R^2 – a^2/4)
Из прямоугольного треугольника LON:
LO/ON = tg 60* = sqrt(3)
OL = sqrt(3)* sqrt(R^2 – a^2/4)
Рассмотрим плоскость верхнего основания:
O1M = sqrt(O1B^2 – BM^2) = (R^2 – (a/2)^2), т.е. O1M = ON
∆O1LM = ∆OLN, отсюда:
OL = O1L
O1L + LO = O1O = a
2sqrt(3) * sqrt(R^2 – a^2/4) = a
12R^2 – 3a^2 = a^2
R = a*sqrt(3)/3
Ответ: a*sqrt(3)/3