Задание
Развернуть задание
При вращении прямоугольника вокруг неравных сторон получаются цилиндры, площади полных поверхностей которых равны S1 и S2. Найдите диагональ прямоугольника.
Развернуть задание
Новое решение
Решение
1) Пусть ABCD искомый прямоугольник, если мы будем вращать его вокруг стороны AB то получим цилиндр, где образующая l=AB=a, а радиус r=AD=b
2) Sосн.=πr2=πb2, Sбок.=2πrl=2πba, Sпол.=2Sосн.+Sбок.=2πb2+2πba=S1 (по условию)
3) Если мы будем вращать вокруг стороны AD то получим цилиндр, где образующая l=AB=b, а радиус r=AB=a
4) Sосн.=πr2=πa2, Sбок.=2πrl=2πab, Sпол.=2Sосн.+Sбок.=2πa2+2πab=S2 (по условию)
5) Получили систему уравнений, найдем a, b.
2πb^2+2πba=S1 ⇔ b(a+b)=S1 ⇔ a+b=S1/b
2πa^2+2πab=S2 ⇔ a(a+b)=S2 ⇔ a+b=S2/a
Значит S1/b =S2/a или b/a= S1/S2
6) Подставим в 1-ое уравнение системы b= aS1/S2. Найдем a2.
2πa^2*S1^2/S2^2+2πa^2*S1/S2=S1
2πa^2*(S1^2/S2^2+S1/S2)=S1
a^2=S1/(2π*(S1S2+S1^2)/S2^2=S1S2^2/
(2πS1*(S2+S1))=S2^2/(2π*(S2+S1))
7) Найдем b^2.
b^2=a^2*S1^2/S2^2= S2^2/(2π*(S2+S1)) * S1^2/S2^2=S1^2/(2π*(S2+S1))
8) Найдем диагональ BD=√(a2+ b2) по теор. Пифагора
BD=√(S2^2/(2π*(S2+S1))+ S1^2/(2π*(S2+S1)))=√((S2^2+S1^2)/(2π*(S2+S1))
Ответ: BD=√((S2^2+S1^2)/(2π*(S2+S1))
2) Sосн.=πr2=πb2, Sбок.=2πrl=2πba, Sпол.=2Sосн.+Sбок.=2πb2+2πba=S1 (по условию)
3) Если мы будем вращать вокруг стороны AD то получим цилиндр, где образующая l=AB=b, а радиус r=AB=a
4) Sосн.=πr2=πa2, Sбок.=2πrl=2πab, Sпол.=2Sосн.+Sбок.=2πa2+2πab=S2 (по условию)
5) Получили систему уравнений, найдем a, b.
2πb^2+2πba=S1 ⇔ b(a+b)=S1 ⇔ a+b=S1/b
2πa^2+2πab=S2 ⇔ a(a+b)=S2 ⇔ a+b=S2/a
Значит S1/b =S2/a или b/a= S1/S2
6) Подставим в 1-ое уравнение системы b= aS1/S2. Найдем a2.
2πa^2*S1^2/S2^2+2πa^2*S1/S2=S1
2πa^2*(S1^2/S2^2+S1/S2)=S1
a^2=S1/(2π*(S1S2+S1^2)/S2^2=S1S2^2/
(2πS1*(S2+S1))=S2^2/(2π*(S2+S1))
7) Найдем b^2.
b^2=a^2*S1^2/S2^2= S2^2/(2π*(S2+S1)) * S1^2/S2^2=S1^2/(2π*(S2+S1))
8) Найдем диагональ BD=√(a2+ b2) по теор. Пифагора
BD=√(S2^2/(2π*(S2+S1))+ S1^2/(2π*(S2+S1)))=√((S2^2+S1^2)/(2π*(S2+S1))
Ответ: BD=√((S2^2+S1^2)/(2π*(S2+S1))
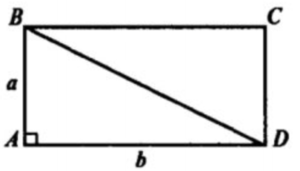
1) Пусть ABCD искомый прямоугольник, если мы будем вращать его вокруг стороны AB то получим цилиндр, где образующая l=AB=a, а радиус r=AD=b
2) Sосн.=πr2=πb2, Sбок.=2πrl=2πba, Sпол.=2Sосн.+Sбок.=2πb2+2πba=S1 (по условию)
3) Если мы будем вращать вокруг стороны AD то получим цилиндр, где образующая l=AB=b, а радиус r=AB=a
4) Sосн.=πr2=πa2, Sбок.=2πrl=2πab, Sпол.=2Sосн.+Sбок.=2πa2+2πab=S2 (по условию)
5) Получили систему уравнений, найдем a, b.
2πb^2+2πba=S1 ⇔ b(a+b)=S1 ⇔ a+b=S1/b
2πa^2+2πab=S2 ⇔ a(a+b)=S2 ⇔ a+b=S2/a
Значит S1/b =S2/a или b/a= S1/S2
6) Подставим в 1-ое уравнение системы b= aS1/S2. Найдем a2.
2πa^2*S1^2/S2^2+2πa^2*S1/S2=S1
2πa^2*(S1^2/S2^2+S1/S2)=S1
a^2=S1/(2π*(S1S2+S1^2)/S2^2=S1S2^2/
(2πS1*(S2+S1))=S2^2/(2π*(S2+S1))
7) Найдем b^2.
b^2=a^2*S1^2/S2^2= S2^2/(2π*(S2+S1)) * S1^2/S2^2=S1^2/(2π*(S2+S1))
8) Найдем диагональ BD=√(a2+ b2) по теор. Пифагора
BD=√(S2^2/(2π*(S2+S1))+ S1^2/(2π*(S2+S1)))=√((S2^2+S1^2)/(2π*(S2+S1))
Ответ: BD=√((S2^2+S1^2)/(2π*(S2+S1))
2) Sосн.=πr2=πb2, Sбок.=2πrl=2πba, Sпол.=2Sосн.+Sбок.=2πb2+2πba=S1 (по условию)
3) Если мы будем вращать вокруг стороны AD то получим цилиндр, где образующая l=AB=b, а радиус r=AB=a
4) Sосн.=πr2=πa2, Sбок.=2πrl=2πab, Sпол.=2Sосн.+Sбок.=2πa2+2πab=S2 (по условию)
5) Получили систему уравнений, найдем a, b.
2πb^2+2πba=S1 ⇔ b(a+b)=S1 ⇔ a+b=S1/b
2πa^2+2πab=S2 ⇔ a(a+b)=S2 ⇔ a+b=S2/a
Значит S1/b =S2/a или b/a= S1/S2
6) Подставим в 1-ое уравнение системы b= aS1/S2. Найдем a2.
2πa^2*S1^2/S2^2+2πa^2*S1/S2=S1
2πa^2*(S1^2/S2^2+S1/S2)=S1
a^2=S1/(2π*(S1S2+S1^2)/S2^2=S1S2^2/
(2πS1*(S2+S1))=S2^2/(2π*(S2+S1))
7) Найдем b^2.
b^2=a^2*S1^2/S2^2= S2^2/(2π*(S2+S1)) * S1^2/S2^2=S1^2/(2π*(S2+S1))
8) Найдем диагональ BD=√(a2+ b2) по теор. Пифагора
BD=√(S2^2/(2π*(S2+S1))+ S1^2/(2π*(S2+S1)))=√((S2^2+S1^2)/(2π*(S2+S1))
Ответ: BD=√((S2^2+S1^2)/(2π*(S2+S1))
