Задание
Развернуть задание
Площадь боковой поверхности цилиндра равна площади круга, описанного около его осевого сечения. Найдите отношение радиуса цилиндра к его высоте.
Развернуть задание
Новое решение
Решение
- Предыдущее
- Следующее
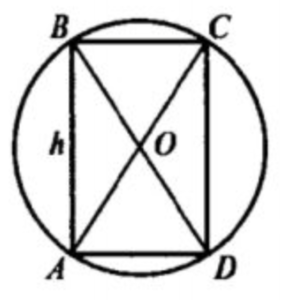
ABCD – прямоугольник, АВ = h, AD = 2r. Пусть AD = a, значит r = a/2. S бок = 2πrh = 2π a/2h = πah
Найдём площадь круга, описанного около осевого сечения:
π*AO^2 = π/4*AC^2
Рассмотрим ∆ACD. По т. Пифагора АС^2 = h^2 + a^2
Площадь круга: π/4*AC^2 = π/4*( h^2 + a^2)
Нужно найти отношение r/6 = a/2h
4ah = h^2+a^2
(a/h)^2 – 4(a/h) + 1 =0
Пусть a/h = t, получили квадратное уравнение: t^2 – 4t + 1=0
D = 16-4 = 12
t 1 = (4 + 2sqtr(3))/2 = 2+sqrt(3)
t 2 = (4 - 2sqtr(3))/2 = 2-sqrt(3)
Значит, получили:
a/2h = t 1,2 / 2 = (2±sqrt(3))/2
Ответ: (2±sqrt(3))/2
Найдём площадь круга, описанного около осевого сечения:
π*AO^2 = π/4*AC^2
Рассмотрим ∆ACD. По т. Пифагора АС^2 = h^2 + a^2
Площадь круга: π/4*AC^2 = π/4*( h^2 + a^2)
Нужно найти отношение r/6 = a/2h
4ah = h^2+a^2
(a/h)^2 – 4(a/h) + 1 =0
Пусть a/h = t, получили квадратное уравнение: t^2 – 4t + 1=0
D = 16-4 = 12
t 1 = (4 + 2sqtr(3))/2 = 2+sqrt(3)
t 2 = (4 - 2sqtr(3))/2 = 2-sqrt(3)
Значит, получили:
a/2h = t 1,2 / 2 = (2±sqrt(3))/2
Ответ: (2±sqrt(3))/2

ABCD – прямоугольник, АВ = h, AD = 2r. Пусть AD = a, значит r = a/2. S бок = 2πrh = 2π a/2h = πah
Найдём площадь круга, описанного около осевого сечения:
π*AO^2 = π/4*AC^2
Рассмотрим ∆ACD. По т. Пифагора АС^2 = h^2 + a^2
Площадь круга: π/4*AC^2 = π/4*( h^2 + a^2)
Нужно найти отношение r/6 = a/2h
4ah = h^2+a^2
(a/h)^2 – 4(a/h) + 1 =0
Пусть a/h = t, получили квадратное уравнение: t^2 – 4t + 1=0
D = 16-4 = 12
t 1 = (4 + 2sqtr(3))/2 = 2+sqrt(3)
t 2 = (4 - 2sqtr(3))/2 = 2-sqrt(3)
Значит, получили:
a/2h = t 1,2 / 2 = (2±sqrt(3))/2
Ответ: (2±sqrt(3))/2
Найдём площадь круга, описанного около осевого сечения:
π*AO^2 = π/4*AC^2
Рассмотрим ∆ACD. По т. Пифагора АС^2 = h^2 + a^2
Площадь круга: π/4*AC^2 = π/4*( h^2 + a^2)
Нужно найти отношение r/6 = a/2h
4ah = h^2+a^2
(a/h)^2 – 4(a/h) + 1 =0
Пусть a/h = t, получили квадратное уравнение: t^2 – 4t + 1=0
D = 16-4 = 12
t 1 = (4 + 2sqtr(3))/2 = 2+sqrt(3)
t 2 = (4 - 2sqtr(3))/2 = 2-sqrt(3)
Значит, получили:
a/2h = t 1,2 / 2 = (2±sqrt(3))/2
Ответ: (2±sqrt(3))/2