Задание
Развернуть задание
Найдите высоту и радиус цилиндра, имеющего наибольшую площадь боковой поверхности, если периметр осевого сечения равен 2p.
Развернуть задание
Новое решение
Решение
1) Пусть осевое сечение цилиндра ABCD- прямоугольник. Высота цилиндра h=AB, радиус основания r=AD/2; Sбок.=2πrh.
2) Периметр прямоугольника ABCD равен 2(AD+AB)=2(2r+h)=2p по условию
3) p=2r+h h=p-2r
4) Sбок.=2πr(p-2r)=2πrp-4πr^2
5) Зададим функцию f(r)=2πrp-4πr^2 r>0 и найдем ее наибольшее значение (наибольшую площадь боковой поверхности)
6) График этой функции парабола с ветками опущенными вниз. Значит максимальное значение достигается в вершине параболы.(xв=-b/2a)
7) -2πp/(-8π)=p/4
8) f(p/4)=2π(p/4)p-4π(p/4)^2=πp^2/2-πp^2/4=πp^2/4 наибольшая площадь боковой поверхности
9) r=p/4; h=p-2r=p-p/2=p/2
Ответ:r=p/4; h=p/2
2) Периметр прямоугольника ABCD равен 2(AD+AB)=2(2r+h)=2p по условию
3) p=2r+h h=p-2r
4) Sбок.=2πr(p-2r)=2πrp-4πr^2
5) Зададим функцию f(r)=2πrp-4πr^2 r>0 и найдем ее наибольшее значение (наибольшую площадь боковой поверхности)
6) График этой функции парабола с ветками опущенными вниз. Значит максимальное значение достигается в вершине параболы.(xв=-b/2a)
7) -2πp/(-8π)=p/4
8) f(p/4)=2π(p/4)p-4π(p/4)^2=πp^2/2-πp^2/4=πp^2/4 наибольшая площадь боковой поверхности
9) r=p/4; h=p-2r=p-p/2=p/2
Ответ:r=p/4; h=p/2
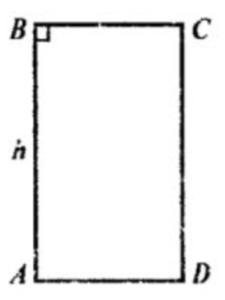
1) Пусть осевое сечение цилиндра ABCD- прямоугольник. Высота цилиндра h=AB, радиус основания r=AD/2; Sбок.=2πrh.
2) Периметр прямоугольника ABCD равен 2(AD+AB)=2(2r+h)=2p по условию
3) p=2r+h h=p-2r
4) Sбок.=2πr(p-2r)=2πrp-4πr^2
5) Зададим функцию f(r)=2πrp-4πr^2 r>0 и найдем ее наибольшее значение (наибольшую площадь боковой поверхности)
6) График этой функции парабола с ветками опущенными вниз. Значит максимальное значение достигается в вершине параболы.(xв=-b/2a)
7) -2πp/(-8π)=p/4
8) f(p/4)=2π(p/4)p-4π(p/4)^2=πp^2/2-πp^2/4=πp^2/4 наибольшая площадь боковой поверхности
9) r=p/4; h=p-2r=p-p/2=p/2
Ответ:r=p/4; h=p/2
2) Периметр прямоугольника ABCD равен 2(AD+AB)=2(2r+h)=2p по условию
3) p=2r+h h=p-2r
4) Sбок.=2πr(p-2r)=2πrp-4πr^2
5) Зададим функцию f(r)=2πrp-4πr^2 r>0 и найдем ее наибольшее значение (наибольшую площадь боковой поверхности)
6) График этой функции парабола с ветками опущенными вниз. Значит максимальное значение достигается в вершине параболы.(xв=-b/2a)
7) -2πp/(-8π)=p/4
8) f(p/4)=2π(p/4)p-4π(p/4)^2=πp^2/2-πp^2/4=πp^2/4 наибольшая площадь боковой поверхности
9) r=p/4; h=p-2r=p-p/2=p/2
Ответ:r=p/4; h=p/2
