Задание
Развернуть задание
Толщина боковой стенки и дна стакана цилиндрической формы равна 1 см, высота стакана равна 16 см, а внутренний радиус равен 5 см. Вычислите площадь полной поверхности стакана.
Развернуть задание
Новое решение
Решение
- Предыдущее
- Следующее
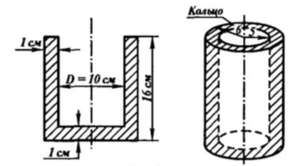
Площадь поверхности стакана будет складываться из площадей внешней и внутренней поверхности стакана.
Найдём площадь внутренней поверхности стакана:
В основании лежит круг r = 5, значит S осн = 25π (см^2)
Высота внутренней части: 16 – 1 = 15 см
Вычислим площадь боковой поверхности:
S бок = 2π*5*15 = 150π (см^2)
Полная площадь внутренней поверхности складывается из площади основания и площади боковой поверхности:
S1 = 25π + 150π = 175π
Найдём площадь внешней поверхности стакана:
Внешний радиус (с учётом толщины стенок) равен 12/2 = 6 см
В основании лежит круг r = 6, значит S осн = 36π (см^2)
Высота стакана 16см
Вычислим площадь боковой поверхности:
S бок = 2π*6*16 = 192π (см^2)
Полная площадь внешней поверхности складывается из площади основания и площади боковой поверхности:
S2 = 36π + 192π = 228π (см^2)
Найдём площадь кольца: S3 = π(36 – 25) = 11π (см^2)
Площадь полной поверхности стакана: 175π + 228π + 11π = 414π (см^2)
Ответ: 414π (см^2)
Найдём площадь внутренней поверхности стакана:
В основании лежит круг r = 5, значит S осн = 25π (см^2)
Высота внутренней части: 16 – 1 = 15 см
Вычислим площадь боковой поверхности:
S бок = 2π*5*15 = 150π (см^2)
Полная площадь внутренней поверхности складывается из площади основания и площади боковой поверхности:
S1 = 25π + 150π = 175π
Найдём площадь внешней поверхности стакана:
Внешний радиус (с учётом толщины стенок) равен 12/2 = 6 см
В основании лежит круг r = 6, значит S осн = 36π (см^2)
Высота стакана 16см
Вычислим площадь боковой поверхности:
S бок = 2π*6*16 = 192π (см^2)
Полная площадь внешней поверхности складывается из площади основания и площади боковой поверхности:
S2 = 36π + 192π = 228π (см^2)
Найдём площадь кольца: S3 = π(36 – 25) = 11π (см^2)
Площадь полной поверхности стакана: 175π + 228π + 11π = 414π (см^2)
Ответ: 414π (см^2)

Площадь поверхности стакана будет складываться из площадей внешней и внутренней поверхности стакана.
Найдём площадь внутренней поверхности стакана:
В основании лежит круг r = 5, значит S осн = 25π (см^2)
Высота внутренней части: 16 – 1 = 15 см
Вычислим площадь боковой поверхности:
S бок = 2π*5*15 = 150π (см^2)
Полная площадь внутренней поверхности складывается из площади основания и площади боковой поверхности:
S1 = 25π + 150π = 175π
Найдём площадь внешней поверхности стакана:
Внешний радиус (с учётом толщины стенок) равен 12/2 = 6 см
В основании лежит круг r = 6, значит S осн = 36π (см^2)
Высота стакана 16см
Вычислим площадь боковой поверхности:
S бок = 2π*6*16 = 192π (см^2)
Полная площадь внешней поверхности складывается из площади основания и площади боковой поверхности:
S2 = 36π + 192π = 228π (см^2)
Найдём площадь кольца: S3 = π(36 – 25) = 11π (см^2)
Площадь полной поверхности стакана: 175π + 228π + 11π = 414π (см^2)
Ответ: 414π (см^2)
Найдём площадь внутренней поверхности стакана:
В основании лежит круг r = 5, значит S осн = 25π (см^2)
Высота внутренней части: 16 – 1 = 15 см
Вычислим площадь боковой поверхности:
S бок = 2π*5*15 = 150π (см^2)
Полная площадь внутренней поверхности складывается из площади основания и площади боковой поверхности:
S1 = 25π + 150π = 175π
Найдём площадь внешней поверхности стакана:
Внешний радиус (с учётом толщины стенок) равен 12/2 = 6 см
В основании лежит круг r = 6, значит S осн = 36π (см^2)
Высота стакана 16см
Вычислим площадь боковой поверхности:
S бок = 2π*6*16 = 192π (см^2)
Полная площадь внешней поверхности складывается из площади основания и площади боковой поверхности:
S2 = 36π + 192π = 228π (см^2)
Найдём площадь кольца: S3 = π(36 – 25) = 11π (см^2)
Площадь полной поверхности стакана: 175π + 228π + 11π = 414π (см^2)
Ответ: 414π (см^2)