Задание
Развернуть задание
Найдите косинус угла при вершине осевого сечения конуса, имеющего три попарно перпендикулярные образующие.
Развернуть задание
Новое решение
Решение
- Предыдущее
- Следующее
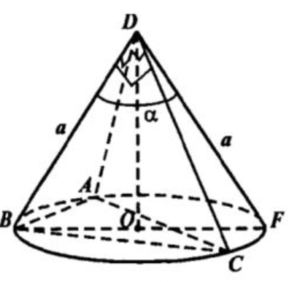
Как известно, образующие конуса равны. Т.е. DA = DB = DC = DF = а
Рассмотрим прямоугольные треугольники DBC, DAB, DAC. Они равны по двум катетам (т.к. DO – общий катет, а OB, OC, OA – радиусы одной и той же окружности).
AB = AC = BC = sqrt(a^2 + a^2) (по теореме Пифагора)
Рассмотрим ∆ABC. По теореме синусов имеем: a*sqrt(2)/sin 60 0 = 2R, отсюда R = a*sqrt(2/3)
BF = 2* a*sqrt(2/3)
Пусть угол BDF = α. Применим теорему косинусов для ∆BDF:
BF^2 = a^2 + a^2 – 2*a*a*cosα
cos α = -1/3
Ответ: cos α = -1/3
Рассмотрим прямоугольные треугольники DBC, DAB, DAC. Они равны по двум катетам (т.к. DO – общий катет, а OB, OC, OA – радиусы одной и той же окружности).
AB = AC = BC = sqrt(a^2 + a^2) (по теореме Пифагора)
Рассмотрим ∆ABC. По теореме синусов имеем: a*sqrt(2)/sin 60 0 = 2R, отсюда R = a*sqrt(2/3)
BF = 2* a*sqrt(2/3)
Пусть угол BDF = α. Применим теорему косинусов для ∆BDF:
BF^2 = a^2 + a^2 – 2*a*a*cosα
cos α = -1/3
Ответ: cos α = -1/3

Как известно, образующие конуса равны. Т.е. DA = DB = DC = DF = а
Рассмотрим прямоугольные треугольники DBC, DAB, DAC. Они равны по двум катетам (т.к. DO – общий катет, а OB, OC, OA – радиусы одной и той же окружности).
AB = AC = BC = sqrt(a^2 + a^2) (по теореме Пифагора)
Рассмотрим ∆ABC. По теореме синусов имеем: a*sqrt(2)/sin 60 0 = 2R, отсюда R = a*sqrt(2/3)
BF = 2* a*sqrt(2/3)
Пусть угол BDF = α. Применим теорему косинусов для ∆BDF:
BF^2 = a^2 + a^2 – 2*a*a*cosα
cos α = -1/3
Ответ: cos α = -1/3
Рассмотрим прямоугольные треугольники DBC, DAB, DAC. Они равны по двум катетам (т.к. DO – общий катет, а OB, OC, OA – радиусы одной и той же окружности).
AB = AC = BC = sqrt(a^2 + a^2) (по теореме Пифагора)
Рассмотрим ∆ABC. По теореме синусов имеем: a*sqrt(2)/sin 60 0 = 2R, отсюда R = a*sqrt(2/3)
BF = 2* a*sqrt(2/3)
Пусть угол BDF = α. Применим теорему косинусов для ∆BDF:
BF^2 = a^2 + a^2 – 2*a*a*cosα
cos α = -1/3
Ответ: cos α = -1/3