Задание
Развернуть задание
Доказать, что сумма расстояний от любой точки, лежащей внутри прямоугольника, до его вершин больше полупериметра прямоугольника.
Развернуть задание
Новое решение
Решение
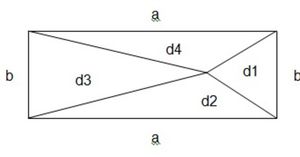
1) d1+d2>b, d2+d3>a, d3+d4>b,
d4+d1>a (по теор. о сумме двух сторон треугольника)
2) Сложим все неравенства:
2(d1+d2+d3+d4)>2(a+b)
3) 2(d1+d2+d3+d4)>P
4) d1+d2+d3+d4>P/2 ч.т.д.
d4+d1>a (по теор. о сумме двух сторон треугольника)
2) Сложим все неравенства:
2(d1+d2+d3+d4)>2(a+b)
3) 2(d1+d2+d3+d4)>P
4) d1+d2+d3+d4>P/2 ч.т.д.
1) d1+d2>b, d2+d3>a, d3+d4>b,
d4+d1>a (по теор. о сумме двух сторон треугольника)
2) Сложим все неравенства:
2(d1+d2+d3+d4)>2(a+b)
3) 2(d1+d2+d3+d4)>P
4) d1+d2+d3+d4>P/2 ч.т.д.
d4+d1>a (по теор. о сумме двух сторон треугольника)
2) Сложим все неравенства:
2(d1+d2+d3+d4)>2(a+b)
3) 2(d1+d2+d3+d4)>P
4) d1+d2+d3+d4>P/2 ч.т.д.
