Задание
Развернуть задание
На сторонах прямоугольного треугольника как на диаметрах построены три полукруга.
Докажите, что площадь полукруга, построенного на гипотенузе, равна сумме площадей полукругов, построенных на катетах.
Докажите, что площадь полукруга, построенного на гипотенузе, равна сумме площадей полукругов, построенных на катетах.
Развернуть задание
Новое решение
Решение
Дано: ∆ABC, ∠C = 90˚, AC – диаметр Окр (O_1, R_1); BC – диаметр Окр (O_2, R_2); AB – диаметр Окр (O_3, R_3)
Доказать: S_3 = S_1 + S_2
Доказательство:
S_3 = 1/2 πR_3 ^2;
S_2 = 1/2 πR_2 ^2;
S_1 = 1/2 πR_1 ^2;
S_1 + S_2 = 1/2 πR_1 ^2 + 1/2 πR_2 ^2 = π/2 * (R_1 ^2
+ R_2 ^2).
По т. Пифагора R_1 ^2 + R_2 ^ 2 = R_3 ^2 => S_1 + S_2 = S_3
Доказать: S_3 = S_1 + S_2
Доказательство:
S_3 = 1/2 πR_3 ^2;
S_2 = 1/2 πR_2 ^2;
S_1 = 1/2 πR_1 ^2;
S_1 + S_2 = 1/2 πR_1 ^2 + 1/2 πR_2 ^2 = π/2 * (R_1 ^2
+ R_2 ^2).
По т. Пифагора R_1 ^2 + R_2 ^ 2 = R_3 ^2 => S_1 + S_2 = S_3
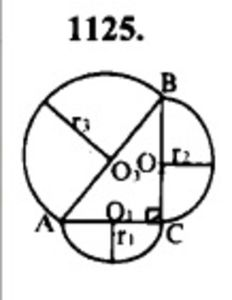
Дано: ∆ABC, ∠C = 90˚, AC – диаметр Окр (O_1, R_1); BC – диаметр Окр (O_2, R_2); AB – диаметр Окр (O_3, R_3)
Доказать: S_3 = S_1 + S_2
Доказательство:
S_3 = 1/2 πR_3 ^2;
S_2 = 1/2 πR_2 ^2;
S_1 = 1/2 πR_1 ^2;
S_1 + S_2 = 1/2 πR_1 ^2 + 1/2 πR_2 ^2 = π/2 * (R_1 ^2
+ R_2 ^2).
По т. Пифагора R_1 ^2 + R_2 ^ 2 = R_3 ^2 => S_1 + S_2 = S_3
Доказать: S_3 = S_1 + S_2
Доказательство:
S_3 = 1/2 πR_3 ^2;
S_2 = 1/2 πR_2 ^2;
S_1 = 1/2 πR_1 ^2;
S_1 + S_2 = 1/2 πR_1 ^2 + 1/2 πR_2 ^2 = π/2 * (R_1 ^2
+ R_2 ^2).
По т. Пифагора R_1 ^2 + R_2 ^ 2 = R_3 ^2 => S_1 + S_2 = S_3
