Чем С2H5OH отличается от С2H6O?
Задание
Развернуть задание
Найдите длину окружности, вписанной в ромб, если:
1) диагонали ромба равны 6 см и 8 см
2) сторона ромба равна a и острый угол равен α
1) диагонали ромба равны 6 см и 8 см
2) сторона ромба равна a и острый угол равен α
Развернуть задание
Новое решение
Решение
Дано: ABCD – ромб описан около Окр (O; R)
Найти: C
Решение:
а) BD = 6 см, AC = 8 см
∆ABO: AO = 4 см, AB = 5 см, BO = 3 см (по т. Пифагора)
S_ABCD = 1/2 * AC * BD = 1/2 * 6 * 8 = 24 см^2
S_ABCD = BC * 2R
24 = 5 * 2R
R = 2.4 см
BB_1 = a * sin α
C = 2πR = 2 * 3.41 * 2.4 = 15.072 см
б) AB = a, ∠A = α
∆ABB_1: ∠B_1 = 90˚, ∠A = α, AB = a
BB_1 = a * sin α
R = 1/2 BB_1 = a * sin α / 2
C = 2πR = πa * sin α
Найти: C
Решение:
а) BD = 6 см, AC = 8 см
∆ABO: AO = 4 см, AB = 5 см, BO = 3 см (по т. Пифагора)
S_ABCD = 1/2 * AC * BD = 1/2 * 6 * 8 = 24 см^2
S_ABCD = BC * 2R
24 = 5 * 2R
R = 2.4 см
BB_1 = a * sin α
C = 2πR = 2 * 3.41 * 2.4 = 15.072 см
б) AB = a, ∠A = α
∆ABB_1: ∠B_1 = 90˚, ∠A = α, AB = a
BB_1 = a * sin α
R = 1/2 BB_1 = a * sin α / 2
C = 2πR = πa * sin α
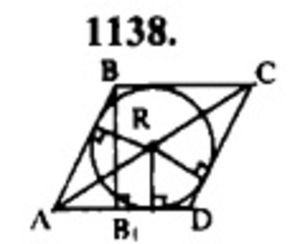
Дано: ABCD – ромб описан около Окр (O; R)
Найти: C
Решение:
а) BD = 6 см, AC = 8 см
∆ABO: AO = 4 см, AB = 5 см, BO = 3 см (по т. Пифагора)
S_ABCD = 1/2 * AC * BD = 1/2 * 6 * 8 = 24 см^2
S_ABCD = BC * 2R
24 = 5 * 2R
R = 2.4 см
BB_1 = a * sin α
C = 2πR = 2 * 3.41 * 2.4 = 15.072 см
б) AB = a, ∠A = α
∆ABB_1: ∠B_1 = 90˚, ∠A = α, AB = a
BB_1 = a * sin α
R = 1/2 BB_1 = a * sin α / 2
C = 2πR = πa * sin α
Найти: C
Решение:
а) BD = 6 см, AC = 8 см
∆ABO: AO = 4 см, AB = 5 см, BO = 3 см (по т. Пифагора)
S_ABCD = 1/2 * AC * BD = 1/2 * 6 * 8 = 24 см^2
S_ABCD = BC * 2R
24 = 5 * 2R
R = 2.4 см
BB_1 = a * sin α
C = 2πR = 2 * 3.41 * 2.4 = 15.072 см
б) AB = a, ∠A = α
∆ABB_1: ∠B_1 = 90˚, ∠A = α, AB = a
BB_1 = a * sin α
R = 1/2 BB_1 = a * sin α / 2
C = 2πR = πa * sin α