Задание
Развернуть задание
Фигура ограничена большими дугами двух окружностей, имеющих общую хорду, длина которой равна 6 см. Для одной окружности эта хорда является стороной вписанного квадрата, для другой – стороной правильного вписанного шестиугольника. Найдите сумму длин этих дуг.
Развернуть задание
Новое решение
Решение
Пусть дана хорда AB = 6 см
Для квадрата a_4 = R_1√2, где a_4 – сторона квадрата, а R_1 – радиус описанной около него окружности, значит, R_1 = a_4/√2 = AB/√2 = 6/√2 = 3√2 см.
Для правильного шестиугольника a_6 = R_2, где a_6 – сторона шестиугольника, а R_2 – радиус описанной около него окружности, значит R_2 = a_6 = 6 см.
Большая длина дуги AB для окружности, к которую вписан квадрат, l_1 = 2πR_1 - 2πR_1/4 = 3πR_1/2; а большая длина дуги AB для окружности, в которую вписан шестиугольник l_2 = 2πR_2 - 2πR_2/6 = 5πR_2/3.
Искомая сумма длин этих дуг:
l_1 + l_2 = 3πR_1/2 + 5πR_2/3 = π(9√2/2 + 5*6/3) = π/2(9√2 + 20) см
Для квадрата a_4 = R_1√2, где a_4 – сторона квадрата, а R_1 – радиус описанной около него окружности, значит, R_1 = a_4/√2 = AB/√2 = 6/√2 = 3√2 см.
Для правильного шестиугольника a_6 = R_2, где a_6 – сторона шестиугольника, а R_2 – радиус описанной около него окружности, значит R_2 = a_6 = 6 см.
Большая длина дуги AB для окружности, к которую вписан квадрат, l_1 = 2πR_1 - 2πR_1/4 = 3πR_1/2; а большая длина дуги AB для окружности, в которую вписан шестиугольник l_2 = 2πR_2 - 2πR_2/6 = 5πR_2/3.
Искомая сумма длин этих дуг:
l_1 + l_2 = 3πR_1/2 + 5πR_2/3 = π(9√2/2 + 5*6/3) = π/2(9√2 + 20) см
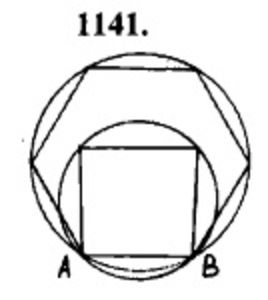
Пусть дана хорда AB = 6 см
Для квадрата a_4 = R_1√2, где a_4 – сторона квадрата, а R_1 – радиус описанной около него окружности, значит, R_1 = a_4/√2 = AB/√2 = 6/√2 = 3√2 см.
Для правильного шестиугольника a_6 = R_2, где a_6 – сторона шестиугольника, а R_2 – радиус описанной около него окружности, значит R_2 = a_6 = 6 см.
Большая длина дуги AB для окружности, к которую вписан квадрат, l_1 = 2πR_1 - 2πR_1/4 = 3πR_1/2; а большая длина дуги AB для окружности, в которую вписан шестиугольник l_2 = 2πR_2 - 2πR_2/6 = 5πR_2/3.
Искомая сумма длин этих дуг:
l_1 + l_2 = 3πR_1/2 + 5πR_2/3 = π(9√2/2 + 5*6/3) = π/2(9√2 + 20) см
Для квадрата a_4 = R_1√2, где a_4 – сторона квадрата, а R_1 – радиус описанной около него окружности, значит, R_1 = a_4/√2 = AB/√2 = 6/√2 = 3√2 см.
Для правильного шестиугольника a_6 = R_2, где a_6 – сторона шестиугольника, а R_2 – радиус описанной около него окружности, значит R_2 = a_6 = 6 см.
Большая длина дуги AB для окружности, к которую вписан квадрат, l_1 = 2πR_1 - 2πR_1/4 = 3πR_1/2; а большая длина дуги AB для окружности, в которую вписан шестиугольник l_2 = 2πR_2 - 2πR_2/6 = 5πR_2/3.
Искомая сумма длин этих дуг:
l_1 + l_2 = 3πR_1/2 + 5πR_2/3 = π(9√2/2 + 5*6/3) = π/2(9√2 + 20) см
