Чем С2H5OH отличается от С2H6O?
Задание
Развернуть задание
Основание трапеции, около которой можно описать окружность, равны 4 см и 14 см, а одна из боковых сторон равна 13 см. Найдите длину описанной окружности.
Развернуть задание
Новое решение
Решение
Дано: ABCD – трапеция, AB = 13 см, AD = 14 см, BC = 4 см
Найти: C
Вокруг трапеции можно описать окружность только в том случае, если ее боковые грани равны друг другу.
AH = (14 – 4)/2 = 5 см
sin A = 5/13,
cos A = √(1 – 25/169) = 12/13
из треугольника ABD:
BD = √(196 + 169 – 2 * 13 * 14 * cos A) = √(365 – 336) = 5
BD/sin A = 2R
R = 5*13/(2*5) = 6.5
C = 2πR = 13π см
Найти: C
Вокруг трапеции можно описать окружность только в том случае, если ее боковые грани равны друг другу.
AH = (14 – 4)/2 = 5 см
sin A = 5/13,
cos A = √(1 – 25/169) = 12/13
из треугольника ABD:
BD = √(196 + 169 – 2 * 13 * 14 * cos A) = √(365 – 336) = 5
BD/sin A = 2R
R = 5*13/(2*5) = 6.5
C = 2πR = 13π см
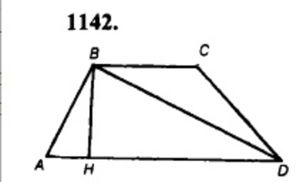
Дано: ABCD – трапеция, AB = 13 см, AD = 14 см, BC = 4 см
Найти: C
Вокруг трапеции можно описать окружность только в том случае, если ее боковые грани равны друг другу.
AH = (14 – 4)/2 = 5 см
sin A = 5/13,
cos A = √(1 – 25/169) = 12/13
из треугольника ABD:
BD = √(196 + 169 – 2 * 13 * 14 * cos A) = √(365 – 336) = 5
BD/sin A = 2R
R = 5*13/(2*5) = 6.5
C = 2πR = 13π см
Найти: C
Вокруг трапеции можно описать окружность только в том случае, если ее боковые грани равны друг другу.
AH = (14 – 4)/2 = 5 см
sin A = 5/13,
cos A = √(1 – 25/169) = 12/13
из треугольника ABD:
BD = √(196 + 169 – 2 * 13 * 14 * cos A) = √(365 – 336) = 5
BD/sin A = 2R
R = 5*13/(2*5) = 6.5
C = 2πR = 13π см