Задание
Развернуть задание
Площадь основания конуса равна S1, а площадь боковой поверхности равна S0. Найдите площадь осевого сечения конуса.
Развернуть задание
Новое решение
Решение
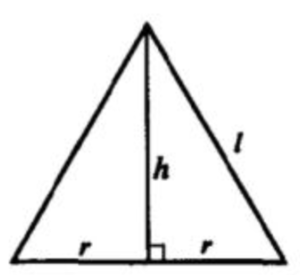
Пусть r-радиус основания конуса, l-его образующая, а h-его высота. Sосн.=S1=πr^2; Sбок.=S0=πrl по условию
l=√(r^2+h^2) по теор. Пифагора. Тогда S0=πr√(r^2+h^2)
Возведем в квадрат S1 и S0. Тогда S1^2=π^2r^4; S0^2=π^2r^2(r^2+h^2)=π^2r^4+π^2r^2h^2=S1^2+π^2r^2h^2 ⇔ π^2r^2h^2=S0^2-S1^2
r^2h^2=(S0^2-S1^2)/π2 ⇔ Sсеч.=rh=√(S0^2-S1^2)/π
Ответ: Sсеч.=√(S0^2-S1^2)/π
l=√(r^2+h^2) по теор. Пифагора. Тогда S0=πr√(r^2+h^2)
Возведем в квадрат S1 и S0. Тогда S1^2=π^2r^4; S0^2=π^2r^2(r^2+h^2)=π^2r^4+π^2r^2h^2=S1^2+π^2r^2h^2 ⇔ π^2r^2h^2=S0^2-S1^2
r^2h^2=(S0^2-S1^2)/π2 ⇔ Sсеч.=rh=√(S0^2-S1^2)/π
Ответ: Sсеч.=√(S0^2-S1^2)/π

Пусть r-радиус основания конуса, l-его образующая, а h-его высота. Sосн.=S1=πr^2; Sбок.=S0=πrl по условию
l=√(r^2+h^2) по теор. Пифагора. Тогда S0=πr√(r^2+h^2)
Возведем в квадрат S1 и S0. Тогда S1^2=π^2r^4; S0^2=π^2r^2(r^2+h^2)=π^2r^4+π^2r^2h^2=S1^2+π^2r^2h^2 ⇔ π^2r^2h^2=S0^2-S1^2
r^2h^2=(S0^2-S1^2)/π2 ⇔ Sсеч.=rh=√(S0^2-S1^2)/π
Ответ: Sсеч.=√(S0^2-S1^2)/π
l=√(r^2+h^2) по теор. Пифагора. Тогда S0=πr√(r^2+h^2)
Возведем в квадрат S1 и S0. Тогда S1^2=π^2r^4; S0^2=π^2r^2(r^2+h^2)=π^2r^4+π^2r^2h^2=S1^2+π^2r^2h^2 ⇔ π^2r^2h^2=S0^2-S1^2
r^2h^2=(S0^2-S1^2)/π2 ⇔ Sсеч.=rh=√(S0^2-S1^2)/π
Ответ: Sсеч.=√(S0^2-S1^2)/π