Задание
Развернуть задание
Отношение площадей боковой и полной поверхностей конуса равно 7/8. Найдите угол между образующей и плоскостью основания конуса.
Развернуть задание
Новое решение
Решение
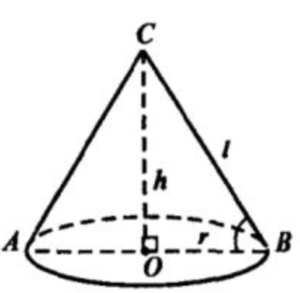
1. Пусть r=OB-радиус основания конуса, l=CB-его образующая.
2. Sосн=πr^2; Sбок.=πrl; Sпол.=Sосн+Sбок=πr^2+πrl=πr(r+l)
3. Sбок/Sпол=⅞ по условию; Sбок/Sпол=πrl/πr(r+l)=l/(r+l)
4. Значит l/(r+l)=⅞ ⇔ 8l=7r+7l ⇔ l=7r ⇔ r/l=1/7
5. cosα=r/l=1/7 по определению косинуса в прямоугольном треугольнике.
Ответ: cosα=1/7
2. Sосн=πr^2; Sбок.=πrl; Sпол.=Sосн+Sбок=πr^2+πrl=πr(r+l)
3. Sбок/Sпол=⅞ по условию; Sбок/Sпол=πrl/πr(r+l)=l/(r+l)
4. Значит l/(r+l)=⅞ ⇔ 8l=7r+7l ⇔ l=7r ⇔ r/l=1/7
5. cosα=r/l=1/7 по определению косинуса в прямоугольном треугольнике.
Ответ: cosα=1/7

1. Пусть r=OB-радиус основания конуса, l=CB-его образующая.
2. Sосн=πr^2; Sбок.=πrl; Sпол.=Sосн+Sбок=πr^2+πrl=πr(r+l)
3. Sбок/Sпол=⅞ по условию; Sбок/Sпол=πrl/πr(r+l)=l/(r+l)
4. Значит l/(r+l)=⅞ ⇔ 8l=7r+7l ⇔ l=7r ⇔ r/l=1/7
5. cosα=r/l=1/7 по определению косинуса в прямоугольном треугольнике.
Ответ: cosα=1/7
2. Sосн=πr^2; Sбок.=πrl; Sпол.=Sосн+Sбок=πr^2+πrl=πr(r+l)
3. Sбок/Sпол=⅞ по условию; Sбок/Sпол=πrl/πr(r+l)=l/(r+l)
4. Значит l/(r+l)=⅞ ⇔ 8l=7r+7l ⇔ l=7r ⇔ r/l=1/7
5. cosα=r/l=1/7 по определению косинуса в прямоугольном треугольнике.
Ответ: cosα=1/7