Задание
Развернуть задание
Через вершину конуса и хорду основания, стягивающую дугу в 120°, проведено сечение, составляющее с плоскостью основания угол в 45°. Найдите площадь сечения, если радиус основания равен 4 см.
Развернуть задание
Новое решение
Решение
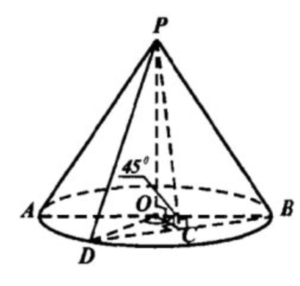
1. Пусть OB=4-радиус основания конуса, ∠DOB=120*, ∠PCO=45*; OC⊥DB
2. PC⊥DB по теор. о 3-x перпендикулярах.
3. △DPB- равнобедренный (DP и PB образующие конуса)
4. DB/sin∠DOB=OB/sin∠BDO ⇔ DB/sin120*=4/sin30* по теор. синусов
5. DB=4sin120*/sin30* ⇔ DB=4(√3/2)/(½)=4√3
6. OC=√(OB^2-BC^2) по теор. Пифагора. Т.к. ОС высота равнобедренного △DOB, то BC=DB/2. Тогда OC=√(OB^2-(DB/2)^2)=√(4^2-(4√3/2)^2)=√(16-12)=2
7. PC=OC/cos∠PCO=2/cos∠45*=2/(√2/2)=4/√2=2√2 по определению косинуса в прямоугольном треугольнике.
8. S△DPB=½*DB*PC=½*4√3*2√2=4√6
Ответ: S△DPB=4√6
2. PC⊥DB по теор. о 3-x перпендикулярах.
3. △DPB- равнобедренный (DP и PB образующие конуса)
4. DB/sin∠DOB=OB/sin∠BDO ⇔ DB/sin120*=4/sin30* по теор. синусов
5. DB=4sin120*/sin30* ⇔ DB=4(√3/2)/(½)=4√3
6. OC=√(OB^2-BC^2) по теор. Пифагора. Т.к. ОС высота равнобедренного △DOB, то BC=DB/2. Тогда OC=√(OB^2-(DB/2)^2)=√(4^2-(4√3/2)^2)=√(16-12)=2
7. PC=OC/cos∠PCO=2/cos∠45*=2/(√2/2)=4/√2=2√2 по определению косинуса в прямоугольном треугольнике.
8. S△DPB=½*DB*PC=½*4√3*2√2=4√6
Ответ: S△DPB=4√6

1. Пусть OB=4-радиус основания конуса, ∠DOB=120*, ∠PCO=45*; OC⊥DB
2. PC⊥DB по теор. о 3-x перпендикулярах.
3. △DPB- равнобедренный (DP и PB образующие конуса)
4. DB/sin∠DOB=OB/sin∠BDO ⇔ DB/sin120*=4/sin30* по теор. синусов
5. DB=4sin120*/sin30* ⇔ DB=4(√3/2)/(½)=4√3
6. OC=√(OB^2-BC^2) по теор. Пифагора. Т.к. ОС высота равнобедренного △DOB, то BC=DB/2. Тогда OC=√(OB^2-(DB/2)^2)=√(4^2-(4√3/2)^2)=√(16-12)=2
7. PC=OC/cos∠PCO=2/cos∠45*=2/(√2/2)=4/√2=2√2 по определению косинуса в прямоугольном треугольнике.
8. S△DPB=½*DB*PC=½*4√3*2√2=4√6
Ответ: S△DPB=4√6
2. PC⊥DB по теор. о 3-x перпендикулярах.
3. △DPB- равнобедренный (DP и PB образующие конуса)
4. DB/sin∠DOB=OB/sin∠BDO ⇔ DB/sin120*=4/sin30* по теор. синусов
5. DB=4sin120*/sin30* ⇔ DB=4(√3/2)/(½)=4√3
6. OC=√(OB^2-BC^2) по теор. Пифагора. Т.к. ОС высота равнобедренного △DOB, то BC=DB/2. Тогда OC=√(OB^2-(DB/2)^2)=√(4^2-(4√3/2)^2)=√(16-12)=2
7. PC=OC/cos∠PCO=2/cos∠45*=2/(√2/2)=4/√2=2√2 по определению косинуса в прямоугольном треугольнике.
8. S△DPB=½*DB*PC=½*4√3*2√2=4√6
Ответ: S△DPB=4√6