Задание
Развернуть задание
Найдите угол между образующей и высотой конуса, если разверткой его боковой поверхности является сектор с дугой 270°.
Развернуть задание
Новое решение
Решение
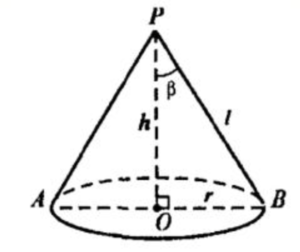
1) Пусть r-радиус основания конуса, l-его образующая.
2) Т.к. α=360*r/l , где α=270*- градусная мера дуги, то r/l =270*/360*=¾
3) sinβ=r/l=¾ по определению синуса в прямоугольном треугольнике. ⇔ β=arcsin¾
Ответ: β=arcsin¾
2) Т.к. α=360*r/l , где α=270*- градусная мера дуги, то r/l =270*/360*=¾
3) sinβ=r/l=¾ по определению синуса в прямоугольном треугольнике. ⇔ β=arcsin¾
Ответ: β=arcsin¾

1) Пусть r-радиус основания конуса, l-его образующая.
2) Т.к. α=360*r/l , где α=270*- градусная мера дуги, то r/l =270*/360*=¾
3) sinβ=r/l=¾ по определению синуса в прямоугольном треугольнике. ⇔ β=arcsin¾
Ответ: β=arcsin¾
2) Т.к. α=360*r/l , где α=270*- градусная мера дуги, то r/l =270*/360*=¾
3) sinβ=r/l=¾ по определению синуса в прямоугольном треугольнике. ⇔ β=arcsin¾
Ответ: β=arcsin¾