Задание
Развернуть задание
Прямоугольный треугольник с катетами а и b вращается вокруг гипотенузы. Найдите площадь поверхности полученного тела.
Развернуть задание
Новое решение
Решение
- Предыдущее
- Следующее
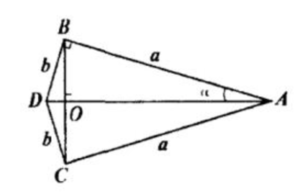
Полученное при вращении тело – два конуса с общим основанием
S бок = πrl
Из ∆ABD по т. Пифагора: DA = sqrt(a^2 + b^2)
sinα = b/ sqrt(a^2 + b^2)
r = ab/ sqrt(a^2 + b^2) = BO
S бок правого конуса: S бок = πrl = S бок = π *ab/ sqrt(a^2 + b^2)*a
S бок левого конуса: S бок = πrl = S бок = π *ab/ sqrt(a^2 + b^2)*b
S = π *ab/ sqrt(a^2 + b^2)*a + π *ab/ sqrt(a^2 + b^2)*b = π *ab*(a+b)/ sqrt(a^2 + b^2)
S бок = πrl
Из ∆ABD по т. Пифагора: DA = sqrt(a^2 + b^2)
sinα = b/ sqrt(a^2 + b^2)
r = ab/ sqrt(a^2 + b^2) = BO
S бок правого конуса: S бок = πrl = S бок = π *ab/ sqrt(a^2 + b^2)*a
S бок левого конуса: S бок = πrl = S бок = π *ab/ sqrt(a^2 + b^2)*b
S = π *ab/ sqrt(a^2 + b^2)*a + π *ab/ sqrt(a^2 + b^2)*b = π *ab*(a+b)/ sqrt(a^2 + b^2)

Полученное при вращении тело – два конуса с общим основанием
S бок = πrl
Из ∆ABD по т. Пифагора: DA = sqrt(a^2 + b^2)
sinα = b/ sqrt(a^2 + b^2)
r = ab/ sqrt(a^2 + b^2) = BO
S бок правого конуса: S бок = πrl = S бок = π *ab/ sqrt(a^2 + b^2)*a
S бок левого конуса: S бок = πrl = S бок = π *ab/ sqrt(a^2 + b^2)*b
S = π *ab/ sqrt(a^2 + b^2)*a + π *ab/ sqrt(a^2 + b^2)*b = π *ab*(a+b)/ sqrt(a^2 + b^2)
S бок = πrl
Из ∆ABD по т. Пифагора: DA = sqrt(a^2 + b^2)
sinα = b/ sqrt(a^2 + b^2)
r = ab/ sqrt(a^2 + b^2) = BO
S бок правого конуса: S бок = πrl = S бок = π *ab/ sqrt(a^2 + b^2)*a
S бок левого конуса: S бок = πrl = S бок = π *ab/ sqrt(a^2 + b^2)*b
S = π *ab/ sqrt(a^2 + b^2)*a + π *ab/ sqrt(a^2 + b^2)*b = π *ab*(a+b)/ sqrt(a^2 + b^2)