Задание
Развернуть задание
Равнобедренная трапеция, основания которой равны 6 см и 10 см, а острый угол 60°, вращается вокруг большего основания. Вычислите площадь поверхности полученного тела.
Развернуть задание
Новое решение
Решение
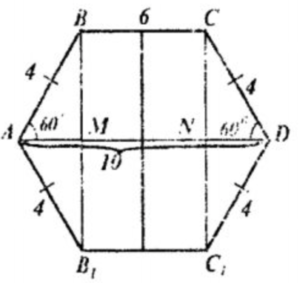
1. Пусть ABСD - искомая равнобедренная трапеция. При вращении вокруг стороны AD получили 2 одинаковых конуса и цилиндр. BC=6, AD=10, ∠DAM=60*. Тогда BM-радиус основания конуса и цилиндра, AB-образующая конуса, CB-образующая цилиндра.
2. 2AM=AD-BC=4; AM=2 по св-ву равнобедренной трапеции.
3. AB=AM/cos60*=2/(½)=4 по опр. косинуса
4. BM=AB*sin60*=4*√3/2=2√3 по опр. синуса
5. Площадь боковой поверхности цилиндра Sбок=2π*BM*CB=2π*2√3*6=24π√3
6. Площадь боковой поверхности конуса Sбок=π*BM*AB=π*2√3*4=8π√3
7. Площадь всей поверхности тела Sпов=Sбок ц +2Sбок к =24π√3+16π√3=40π√3
Ответ: Sпов=40π√3
2. 2AM=AD-BC=4; AM=2 по св-ву равнобедренной трапеции.
3. AB=AM/cos60*=2/(½)=4 по опр. косинуса
4. BM=AB*sin60*=4*√3/2=2√3 по опр. синуса
5. Площадь боковой поверхности цилиндра Sбок=2π*BM*CB=2π*2√3*6=24π√3
6. Площадь боковой поверхности конуса Sбок=π*BM*AB=π*2√3*4=8π√3
7. Площадь всей поверхности тела Sпов=Sбок ц +2Sбок к =24π√3+16π√3=40π√3
Ответ: Sпов=40π√3

1. Пусть ABСD - искомая равнобедренная трапеция. При вращении вокруг стороны AD получили 2 одинаковых конуса и цилиндр. BC=6, AD=10, ∠DAM=60*. Тогда BM-радиус основания конуса и цилиндра, AB-образующая конуса, CB-образующая цилиндра.
2. 2AM=AD-BC=4; AM=2 по св-ву равнобедренной трапеции.
3. AB=AM/cos60*=2/(½)=4 по опр. косинуса
4. BM=AB*sin60*=4*√3/2=2√3 по опр. синуса
5. Площадь боковой поверхности цилиндра Sбок=2π*BM*CB=2π*2√3*6=24π√3
6. Площадь боковой поверхности конуса Sбок=π*BM*AB=π*2√3*4=8π√3
7. Площадь всей поверхности тела Sпов=Sбок ц +2Sбок к =24π√3+16π√3=40π√3
Ответ: Sпов=40π√3
2. 2AM=AD-BC=4; AM=2 по св-ву равнобедренной трапеции.
3. AB=AM/cos60*=2/(½)=4 по опр. косинуса
4. BM=AB*sin60*=4*√3/2=2√3 по опр. синуса
5. Площадь боковой поверхности цилиндра Sбок=2π*BM*CB=2π*2√3*6=24π√3
6. Площадь боковой поверхности конуса Sбок=π*BM*AB=π*2√3*4=8π√3
7. Площадь всей поверхности тела Sпов=Sбок ц +2Sбок к =24π√3+16π√3=40π√3
Ответ: Sпов=40π√3