Задание
Развернуть задание
Высота конуса равна 4 см, а радиус основания равен 3 см. Вычислите площадь полной поверхности правильной n-угольной пирамиды, вписанной в конус, если:
а) n = 3;
б) n= 4;
в) n = 6.
а) n = 3;
б) n= 4;
в) n = 6.
Развернуть задание
Новое решение
Решение
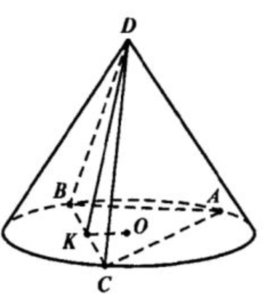
а) 1. Пусть OK⊥BC, R=3-радиус основания конуса, h=DO=4-его высота.
2. DK⊥BCпо теор. о 3-х перпендикулрах (OK⊥BC, OK⊥OD)
3. Т.к.△ABC правильный, то ОK=r радиус вписанной окружности в △ABC
4. Sосн=S△ABC=pr; p-полупериметр △ABC
5. AB/sin∠ACB=2R по теор. cинусов ⇔ ⇔AB=2R*sin∠ACB=2R*sin60*=2*3*√3/2=3√3
6. AB=BC=AC т.к. △ABC правильный; p=(AB+BC+AC)/2=3AB/2=9√3/2
7. S△ABC=½*AB*BC*sin∠CAB=½*AB^2*sin60*=½*27*√3/2=27√3/4
8. Тогда r=S△ABC/p=27√3/4/(9√3/2)=(2*27√3)/(9√3*4)=3/2
9. DK=√(DO^2+KO^2)=√(4^2+(3/2)^2)=√(16+9/4)=√73/2 по теор. Пифагора
10. S△BDC=½*DK*BC=½*√73/2*3√3=¾*√219
11. Sбок=3S△BDC=3*¾*√219=9/4*√219
12. Sпол=Sбок+Sосн=9/4*√219+27√3/4=9√3/4*(√73+3)
Ответ:Sпол=9√3/4*(√73+3)
2. DK⊥BCпо теор. о 3-х перпендикулрах (OK⊥BC, OK⊥OD)
3. Т.к.△ABC правильный, то ОK=r радиус вписанной окружности в △ABC
4. Sосн=S△ABC=pr; p-полупериметр △ABC
5. AB/sin∠ACB=2R по теор. cинусов ⇔ ⇔AB=2R*sin∠ACB=2R*sin60*=2*3*√3/2=3√3
6. AB=BC=AC т.к. △ABC правильный; p=(AB+BC+AC)/2=3AB/2=9√3/2
7. S△ABC=½*AB*BC*sin∠CAB=½*AB^2*sin60*=½*27*√3/2=27√3/4
8. Тогда r=S△ABC/p=27√3/4/(9√3/2)=(2*27√3)/(9√3*4)=3/2
9. DK=√(DO^2+KO^2)=√(4^2+(3/2)^2)=√(16+9/4)=√73/2 по теор. Пифагора
10. S△BDC=½*DK*BC=½*√73/2*3√3=¾*√219
11. Sбок=3S△BDC=3*¾*√219=9/4*√219
12. Sпол=Sбок+Sосн=9/4*√219+27√3/4=9√3/4*(√73+3)
Ответ:Sпол=9√3/4*(√73+3)
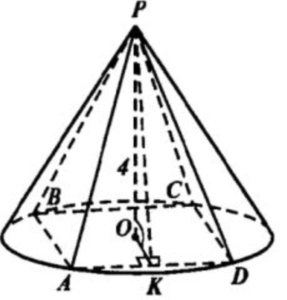
б) 1. Пусть OK⊥AD, R=3-радиус основания конуса, h=PO=4-его высота.
2. PK⊥ADпо теор. о 3-х перпендикулрах (OK⊥AD, OK⊥OP)
3. BD=2R=6 (диагональ квдрата равна диаметру описаной около него окружности)
4. a=BD/√2=6/√2=3√2 сторона квадрата
5. Sоcн=a2=(3√2)2=18
6. ОK=r=a/2=3√2/2 радиус вписанной окружности
7. PK=√(PO^2+KO^2)=√(4^2+(3√2/2)^2)=√(16+9/2)=√(41/2) по теор. Пифагора
8. S△APD=½*PK*AD=½*PK*a=½*√(41/2)*3√2=3/2*√41
9. Sбок=4S△APD=4*3/2*√41=6√41
10. Sпол=Sбок+Sосн=6√41+18=6*(√41+3)
Ответ:Sпол=6*(√41+3)
2. PK⊥ADпо теор. о 3-х перпендикулрах (OK⊥AD, OK⊥OP)
3. BD=2R=6 (диагональ квдрата равна диаметру описаной около него окружности)
4. a=BD/√2=6/√2=3√2 сторона квадрата
5. Sоcн=a2=(3√2)2=18
6. ОK=r=a/2=3√2/2 радиус вписанной окружности
7. PK=√(PO^2+KO^2)=√(4^2+(3√2/2)^2)=√(16+9/2)=√(41/2) по теор. Пифагора
8. S△APD=½*PK*AD=½*PK*a=½*√(41/2)*3√2=3/2*√41
9. Sбок=4S△APD=4*3/2*√41=6√41
10. Sпол=Sбок+Sосн=6√41+18=6*(√41+3)
Ответ:Sпол=6*(√41+3)
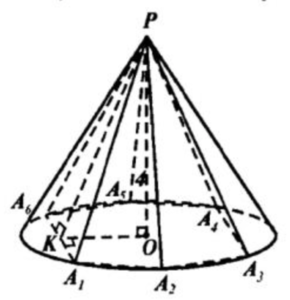
в)
1. Пусть OK⊥A1A6, R=3-радиус основания конуса, h=PO=4-его высота.
2. PK⊥A1A6по теор. о 3-х перпендикулрах (OK⊥A1A6, OK⊥OP)
3. a=R=3 сторона правильного шестиугольника
4. ОK=r радиус вписанной окружности r=√(A1*O^2-K*A1^2)=√(a^2-a^2/4)=a√3/2=3√3/2
5. PK=√(PO2+KO2)=√(42+(3√3/2)2)=√(16+27/4)=√91/2 по теор. Пифагора
6. △OA1A6 - равностороний, поэтому S△OA1A6=a^2√3/4=9√3/4
7. Sоcн=6S△OA1A6=6*9√3/4=27√3/2
8. S△PA1A6=½*PK*A1A6=½*PK*a=½*√91/2*3=3/4*√91
9. Sбок=6S△PA1A6=6*3/4*√91=9/2√91
10. Sпол=Sбок+Sосн=9/2√91+27√3/2=9/2*(√91+3√3)
Ответ:Sпол=9/2*(√91+3√3)
1. Пусть OK⊥A1A6, R=3-радиус основания конуса, h=PO=4-его высота.
2. PK⊥A1A6по теор. о 3-х перпендикулрах (OK⊥A1A6, OK⊥OP)
3. a=R=3 сторона правильного шестиугольника
4. ОK=r радиус вписанной окружности r=√(A1*O^2-K*A1^2)=√(a^2-a^2/4)=a√3/2=3√3/2
5. PK=√(PO2+KO2)=√(42+(3√3/2)2)=√(16+27/4)=√91/2 по теор. Пифагора
6. △OA1A6 - равностороний, поэтому S△OA1A6=a^2√3/4=9√3/4
7. Sоcн=6S△OA1A6=6*9√3/4=27√3/2
8. S△PA1A6=½*PK*A1A6=½*PK*a=½*√91/2*3=3/4*√91
9. Sбок=6S△PA1A6=6*3/4*√91=9/2√91
10. Sпол=Sбок+Sосн=9/2√91+27√3/2=9/2*(√91+3√3)
Ответ:Sпол=9/2*(√91+3√3)

а) 1. Пусть OK⊥BC, R=3-радиус основания конуса, h=DO=4-его высота.
2. DK⊥BCпо теор. о 3-х перпендикулрах (OK⊥BC, OK⊥OD)
3. Т.к.△ABC правильный, то ОK=r радиус вписанной окружности в △ABC
4. Sосн=S△ABC=pr; p-полупериметр △ABC
5. AB/sin∠ACB=2R по теор. cинусов ⇔ ⇔AB=2R*sin∠ACB=2R*sin60*=2*3*√3/2=3√3
6. AB=BC=AC т.к. △ABC правильный; p=(AB+BC+AC)/2=3AB/2=9√3/2
7. S△ABC=½*AB*BC*sin∠CAB=½*AB^2*sin60*=½*27*√3/2=27√3/4
8. Тогда r=S△ABC/p=27√3/4/(9√3/2)=(2*27√3)/(9√3*4)=3/2
9. DK=√(DO^2+KO^2)=√(4^2+(3/2)^2)=√(16+9/4)=√73/2 по теор. Пифагора
10. S△BDC=½*DK*BC=½*√73/2*3√3=¾*√219
11. Sбок=3S△BDC=3*¾*√219=9/4*√219
12. Sпол=Sбок+Sосн=9/4*√219+27√3/4=9√3/4*(√73+3)
Ответ:Sпол=9√3/4*(√73+3)
2. DK⊥BCпо теор. о 3-х перпендикулрах (OK⊥BC, OK⊥OD)
3. Т.к.△ABC правильный, то ОK=r радиус вписанной окружности в △ABC
4. Sосн=S△ABC=pr; p-полупериметр △ABC
5. AB/sin∠ACB=2R по теор. cинусов ⇔ ⇔AB=2R*sin∠ACB=2R*sin60*=2*3*√3/2=3√3
6. AB=BC=AC т.к. △ABC правильный; p=(AB+BC+AC)/2=3AB/2=9√3/2
7. S△ABC=½*AB*BC*sin∠CAB=½*AB^2*sin60*=½*27*√3/2=27√3/4
8. Тогда r=S△ABC/p=27√3/4/(9√3/2)=(2*27√3)/(9√3*4)=3/2
9. DK=√(DO^2+KO^2)=√(4^2+(3/2)^2)=√(16+9/4)=√73/2 по теор. Пифагора
10. S△BDC=½*DK*BC=½*√73/2*3√3=¾*√219
11. Sбок=3S△BDC=3*¾*√219=9/4*√219
12. Sпол=Sбок+Sосн=9/4*√219+27√3/4=9√3/4*(√73+3)
Ответ:Sпол=9√3/4*(√73+3)

б) 1. Пусть OK⊥AD, R=3-радиус основания конуса, h=PO=4-его высота.
2. PK⊥ADпо теор. о 3-х перпендикулрах (OK⊥AD, OK⊥OP)
3. BD=2R=6 (диагональ квдрата равна диаметру описаной около него окружности)
4. a=BD/√2=6/√2=3√2 сторона квадрата
5. Sоcн=a2=(3√2)2=18
6. ОK=r=a/2=3√2/2 радиус вписанной окружности
7. PK=√(PO^2+KO^2)=√(4^2+(3√2/2)^2)=√(16+9/2)=√(41/2) по теор. Пифагора
8. S△APD=½*PK*AD=½*PK*a=½*√(41/2)*3√2=3/2*√41
9. Sбок=4S△APD=4*3/2*√41=6√41
10. Sпол=Sбок+Sосн=6√41+18=6*(√41+3)
Ответ:Sпол=6*(√41+3)
2. PK⊥ADпо теор. о 3-х перпендикулрах (OK⊥AD, OK⊥OP)
3. BD=2R=6 (диагональ квдрата равна диаметру описаной около него окружности)
4. a=BD/√2=6/√2=3√2 сторона квадрата
5. Sоcн=a2=(3√2)2=18
6. ОK=r=a/2=3√2/2 радиус вписанной окружности
7. PK=√(PO^2+KO^2)=√(4^2+(3√2/2)^2)=√(16+9/2)=√(41/2) по теор. Пифагора
8. S△APD=½*PK*AD=½*PK*a=½*√(41/2)*3√2=3/2*√41
9. Sбок=4S△APD=4*3/2*√41=6√41
10. Sпол=Sбок+Sосн=6√41+18=6*(√41+3)
Ответ:Sпол=6*(√41+3)

в)
1. Пусть OK⊥A1A6, R=3-радиус основания конуса, h=PO=4-его высота.
2. PK⊥A1A6по теор. о 3-х перпендикулрах (OK⊥A1A6, OK⊥OP)
3. a=R=3 сторона правильного шестиугольника
4. ОK=r радиус вписанной окружности r=√(A1*O^2-K*A1^2)=√(a^2-a^2/4)=a√3/2=3√3/2
5. PK=√(PO2+KO2)=√(42+(3√3/2)2)=√(16+27/4)=√91/2 по теор. Пифагора
6. △OA1A6 - равностороний, поэтому S△OA1A6=a^2√3/4=9√3/4
7. Sоcн=6S△OA1A6=6*9√3/4=27√3/2
8. S△PA1A6=½*PK*A1A6=½*PK*a=½*√91/2*3=3/4*√91
9. Sбок=6S△PA1A6=6*3/4*√91=9/2√91
10. Sпол=Sбок+Sосн=9/2√91+27√3/2=9/2*(√91+3√3)
Ответ:Sпол=9/2*(√91+3√3)
1. Пусть OK⊥A1A6, R=3-радиус основания конуса, h=PO=4-его высота.
2. PK⊥A1A6по теор. о 3-х перпендикулрах (OK⊥A1A6, OK⊥OP)
3. a=R=3 сторона правильного шестиугольника
4. ОK=r радиус вписанной окружности r=√(A1*O^2-K*A1^2)=√(a^2-a^2/4)=a√3/2=3√3/2
5. PK=√(PO2+KO2)=√(42+(3√3/2)2)=√(16+27/4)=√91/2 по теор. Пифагора
6. △OA1A6 - равностороний, поэтому S△OA1A6=a^2√3/4=9√3/4
7. Sоcн=6S△OA1A6=6*9√3/4=27√3/2
8. S△PA1A6=½*PK*A1A6=½*PK*a=½*√91/2*3=3/4*√91
9. Sбок=6S△PA1A6=6*3/4*√91=9/2√91
10. Sпол=Sбок+Sосн=9/2√91+27√3/2=9/2*(√91+3√3)
Ответ:Sпол=9/2*(√91+3√3)