Задание
Развернуть задание
Диагонали осевого сечения усеченного конуса перпендикулярны. Одно из оснований осевого сечения равно 40 см, а его площадь равна 36 дм2. Вычислите площади боковой и полной поверхностей усеченного конуса.
Развернуть задание
Новое решение
Решение
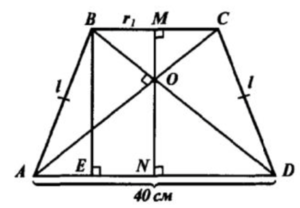
1. ABCD-трапеция, осевое сечение усеченного конуса; SABCD=36дм^2; AD=40см.
Пусть R1- 1-ый радиус основания усеченного конуса.
Пусть R2=1/2AD=20cм - 2-ый радиус основания усеченного конуса.
l = AB- образующая конуса
2. MN-высота трапеции равная средней линии т.к. диагонали трапеции взаимно перпендикуляры. MN=(BC+AD)/2=(2R1+40)/2=R1+20 см
3. SABCD=(BC+AD)/2*MN=MN^2 ⇔ MN^2=3600 ⇔ MN=60cм
4. Значит R1+20=60 ⇔ R1=40. Но BC=2R1=80см. Значит этот рисунок не правильный, изменим его.
Пусть R1- 1-ый радиус основания усеченного конуса.
Пусть R2=1/2AD=20cм - 2-ый радиус основания усеченного конуса.
l = AB- образующая конуса
2. MN-высота трапеции равная средней линии т.к. диагонали трапеции взаимно перпендикуляры. MN=(BC+AD)/2=(2R1+40)/2=R1+20 см
3. SABCD=(BC+AD)/2*MN=MN^2 ⇔ MN^2=3600 ⇔ MN=60cм
4. Значит R1+20=60 ⇔ R1=40. Но BC=2R1=80см. Значит этот рисунок не правильный, изменим его.
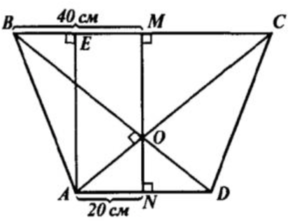
1. Пусть AB⊥BC, значит BE=40-20=20 см. AE-высота трапеции AE=MN=60cм.
2. AB=√(AE^2+BE^2)=√(60^2+20^2)=√(3600+400)=√4000=20√10 cм.
3. Sбок=π(R1+R2)l=π(40+20)AB=60π*20√10=1200√10*π cм^2.
4. Sосн 1=π*R1^2=π*40^2=1600π cм2. Sосн 2=π*R2^2=π*20^2=400π cм^2.
5. Sпов=Sбок+Sосн 1+Sосн 2=π(R1+R2)l=1200√10*π+1600π+400π=1200√10*π+2000π (см^2) или Sпов=12√10*π+20π (дм^2)
Ответ: Sпов=12√10*π+20π (дм^2)
2. AB=√(AE^2+BE^2)=√(60^2+20^2)=√(3600+400)=√4000=20√10 cм.
3. Sбок=π(R1+R2)l=π(40+20)AB=60π*20√10=1200√10*π cм^2.
4. Sосн 1=π*R1^2=π*40^2=1600π cм2. Sосн 2=π*R2^2=π*20^2=400π cм^2.
5. Sпов=Sбок+Sосн 1+Sосн 2=π(R1+R2)l=1200√10*π+1600π+400π=1200√10*π+2000π (см^2) или Sпов=12√10*π+20π (дм^2)
Ответ: Sпов=12√10*π+20π (дм^2)

1. ABCD-трапеция, осевое сечение усеченного конуса; SABCD=36дм^2; AD=40см.
Пусть R1- 1-ый радиус основания усеченного конуса.
Пусть R2=1/2AD=20cм - 2-ый радиус основания усеченного конуса.
l = AB- образующая конуса
2. MN-высота трапеции равная средней линии т.к. диагонали трапеции взаимно перпендикуляры. MN=(BC+AD)/2=(2R1+40)/2=R1+20 см
3. SABCD=(BC+AD)/2*MN=MN^2 ⇔ MN^2=3600 ⇔ MN=60cм
4. Значит R1+20=60 ⇔ R1=40. Но BC=2R1=80см. Значит этот рисунок не правильный, изменим его.
Пусть R1- 1-ый радиус основания усеченного конуса.
Пусть R2=1/2AD=20cм - 2-ый радиус основания усеченного конуса.
l = AB- образующая конуса
2. MN-высота трапеции равная средней линии т.к. диагонали трапеции взаимно перпендикуляры. MN=(BC+AD)/2=(2R1+40)/2=R1+20 см
3. SABCD=(BC+AD)/2*MN=MN^2 ⇔ MN^2=3600 ⇔ MN=60cм
4. Значит R1+20=60 ⇔ R1=40. Но BC=2R1=80см. Значит этот рисунок не правильный, изменим его.

1. Пусть AB⊥BC, значит BE=40-20=20 см. AE-высота трапеции AE=MN=60cм.
2. AB=√(AE^2+BE^2)=√(60^2+20^2)=√(3600+400)=√4000=20√10 cм.
3. Sбок=π(R1+R2)l=π(40+20)AB=60π*20√10=1200√10*π cм^2.
4. Sосн 1=π*R1^2=π*40^2=1600π cм2. Sосн 2=π*R2^2=π*20^2=400π cм^2.
5. Sпов=Sбок+Sосн 1+Sосн 2=π(R1+R2)l=1200√10*π+1600π+400π=1200√10*π+2000π (см^2) или Sпов=12√10*π+20π (дм^2)
Ответ: Sпов=12√10*π+20π (дм^2)
2. AB=√(AE^2+BE^2)=√(60^2+20^2)=√(3600+400)=√4000=20√10 cм.
3. Sбок=π(R1+R2)l=π(40+20)AB=60π*20√10=1200√10*π cм^2.
4. Sосн 1=π*R1^2=π*40^2=1600π cм2. Sосн 2=π*R2^2=π*20^2=400π cм^2.
5. Sпов=Sбок+Sосн 1+Sосн 2=π(R1+R2)l=1200√10*π+1600π+400π=1200√10*π+2000π (см^2) или Sпов=12√10*π+20π (дм^2)
Ответ: Sпов=12√10*π+20π (дм^2)