Решения
Ольга


01-12-2016 14:19

0
Задания
Задание
Лолита
28-11-2016
14:20
Школа

Геометрия

11 класс


11
1
0
0

Шар и сфера, их сечения

Доказать (центр сферы), найти расстояние от центра сферы до плоскости

Развернуть задание
Вершины прямоугольного треугольника с катетами 1,8 см и 2,4 см лежат на сфере, а) Докажите, что если радиус сферы равен 1,5 см, то центр сферы лежит в плоскости треугольника. б) Найдите расстояние от центра сферы до плоскости треугольника, если радиус сферы равен 6,5 см.
Сергей Геннадиевич
Новый коммент
24-07-2017 17:41:17
Алиса
Судя по таблице удельной теплоёмкости, это может быть цинк.
22-11-2016 12:57:23
Анастасия
Дмитрий Да, перевод обязателен.
21-11-2016 19:00:39
Дмитрий
1) –Обязательно ли переводить массу мяча в СИ?
21-11-2016 18:51:12
Рогова Дарья
Условие смущает. Ладно, пусть время будет отрицательным, наблюдать можно с любого момента, но не ясно, каким моментам времени соответствуют моменты изменения скорости. Можно предположить, что первый пик где-то в районе -1,5 с, но так ли это?.. Третий пик вообще без координатной сетки не определишь. И еще: график чего именно надо построить? МОДУЛЯ скорости или ПРОЕКЦИИ скорости?
3-11-2016 00:11:19
Андрей Анатольевич
Почему картика в блоке так размыта? А при просмотре в правой части (крупно) все выглядит гораздо лучше. Как то плохо пережимается картинка.
2-11-2016 15:29:02
Андрей Анатольевич
t = 20ºC или 200 С ?
31-10-2016 20:21:46
Эдуард Блохин
Интересное задание. Пригодится.
27-10-2016 14:34:02
Развернуть задание
Новое решение
Сложность
4 3 2 1
Решение
Ольга
1-12-2016 14:19:52
0
а) Найдем гипотенузу по теор. Пифагора c=√(1,82+2,42)= √(3,24+5,76)=√9=3 см. r=1,5см радиус сферы, d=2r=2*1,5=3 см диаметр сферы. Значит с=d и центр сферы находится на середине гипотенузы => лежит в плоскости треугольника.
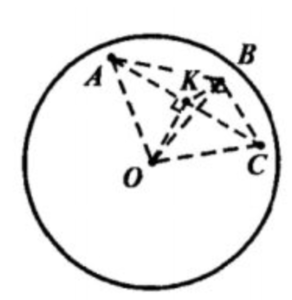
б)Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы. Проведем из точки О отрезок ОК ⊥ плоскости ΔАВС, это отрезки КА, КВ, КС. Равные наклонные (радиусы ОА, ОВ, ОС) имеют равные проекции на плоскость АВС, тогда, КА=КВ=КС т.к. равные наклонные (радиусы ОА, ОВ, ОС) имеют равные проекции на плоскость АВС, точка К равноудалена от вершин ΔАВС, значит, она — центр описанной окружности. Таким образом, точка К — середина гипотенузы АС; AK=1/2AC=1,5cм.OA=6,5см по условию. ОК — искомое расстояние. ОК=√(OA^2+KA^2)= =√(6,5^2+1,5^2)=√(42,25+2,25)=√40=2√10 по теореме Пифагора.
Ответ: ОК=2√10
Алиса
Ира Использовали теорему Пифагора для прямоугольного треугольника МСН.
6-12-2016 22:54:04
Ира
Откуда взяли, что MH = √(28 + 8) = 6 см?
6-12-2016 22:52:55
Sh Polina
Катя Так как исходный треугольник равнобедренный и прямоугольный, значит угол В = 45˚.
Из прямоугольного треугольника sin 45˚=СН/СВ
6-12-2016 22:51:34
Катя
Почему CH = BC * sin 45˚?
6-12-2016 22:50:12
Sh Polina
Анастасия Использовали теорему Пифагора к прямоугольному ∆MCH
6-12-2016 22:49:03
Анастасия
Как мы определили, что p(M, AB) = MH = √(MC^2 + CH^2)?
6-12-2016 22:48:12
Sh Polina
Анастасия Так как BD – диагональ квадрата, то по свойству диагонали квадрата BD = AB * √2
6-12-2016 22:45:40
Sh Polina
Елизавета Использовали теорему Пифагора к прямоугольному ∆ABF
6-12-2016 22:45:18
Анастасия
Почему BD = AB * √2?
6-12-2016 22:43:41
Елизавета
Как мы определили, что p(F, AD) = √(FB^2 + AB^2)?
6-12-2016 22:42:38
Елизавета
Анастасия Так как треугольник ABC – правильный, значит он является равнобедренным, а в равнобедренном треугольнике медиана, биссектриса и высота, проведённые к основанию, совпадают.
6-12-2016 22:39:01
Анастасия
В решении написано, что если AM – медиана в ∆ABC, то MA ⊥ BC. Откуда это взялось?
6-12-2016 22:38:06
Елизавета
Катя По лемме о перпендикулярных прямых (если одна из двух параллельных прямых перпендикулярна к третьей, то и другая прямая перпендикулярна к этой прямой)
6-12-2016 22:35:27
Катя
Почему если a ⊥ d1, d1 || d то из этого следует, что a ⊥ d?
6-12-2016 22:34:38
Елизавета
Алиса Было сказано, что ∆АВС – равнобедренный, а по свойству равнобедренного треугольника, биссектриса, медиана и высота, проведенные к основанию, совпадают.
6-12-2016 22:31:20
Алиса
Почему мы решили, что если AM – медиана, то она и высота?
6-12-2016 22:29:37
Даша
Диана Это прямая, перпендикулярная к данному отрезку и проходящая через его середину.
6-12-2016 21:51:31
Диана
Что такое серединный перпендикуляр?
6-12-2016 21:51:03
Диана
Ольга Сумма углов в треугольнике равна 180˚. Так как ∠A + ∠B = 90˚, то на угол С остаётся 90˚
6-12-2016 21:46:59
Ольга
Как получилось, что ∠С = 90˚?
6-12-2016 21:46:22
Ольга
1-12-2016 14:19:52
0
а) Найдем гипотенузу по теор. Пифагора c=√(1,82+2,42)= √(3,24+5,76)=√9=3 см. r=1,5см радиус сферы, d=2r=2*1,5=3 см диаметр сферы. Значит с=d и центр сферы находится на середине гипотенузы => лежит в плоскости треугольника.
б)Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы. Проведем из точки О отрезок ОК ⊥ плоскости ΔАВС, это отрезки КА, КВ, КС. Равные наклонные (радиусы ОА, ОВ, ОС) имеют равные проекции на плоскость АВС, тогда, КА=КВ=КС т.к. равные наклонные (радиусы ОА, ОВ, ОС) имеют равные проекции на плоскость АВС, точка К равноудалена от вершин ΔАВС, значит, она — центр описанной окружности. Таким образом, точка К — середина гипотенузы АС; AK=1/2AC=1,5cм.OA=6,5см по условию. ОК — искомое расстояние. ОК=√(OA^2+KA^2)= =√(6,5^2+1,5^2)=√(42,25+2,25)=√40=2√10 по теореме Пифагора.
Ответ: ОК=2√10
Новость часа

Форма обратной связи