Задание
Развернуть задание
В арифметической прогрессии a1+a5=5/3 a3a4=65/72. Найти сумму семнадцати первых членов прогрессии.
Развернуть задание
Новое решение
Решение
1. По условию a1+a5=5/3 a3*a4=65/72.
2. Так как an=a1+(n-1)d, то a5=a1+4d, a4=a1+3d, a3=a1+2d
3. Составим систему уравнений:
2. Так как an=a1+(n-1)d, то a5=a1+4d, a4=a1+3d, a3=a1+2d
3. Составим систему уравнений:
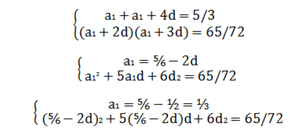
25/36-(10/3)d+4d^2+(25/6)d-10d^2+6d^2=65/72<=> (5/6)d=15/72 <=> d=1/4
4. Так как Sn=(2a1+(n-1)d)/2*n , то S17=(2/3+16/4)/2*17=(1/3+2)*17=5(2/3)+34=39(2/3) .
Ответ: S17=39(2/3).
4. Так как Sn=(2a1+(n-1)d)/2*n , то S17=(2/3+16/4)/2*17=(1/3+2)*17=5(2/3)+34=39(2/3) .
Ответ: S17=39(2/3).
1. По условию a1+a5=5/3 a3*a4=65/72.
2. Так как an=a1+(n-1)d, то a5=a1+4d, a4=a1+3d, a3=a1+2d
3. Составим систему уравнений:
2. Так как an=a1+(n-1)d, то a5=a1+4d, a4=a1+3d, a3=a1+2d
3. Составим систему уравнений:
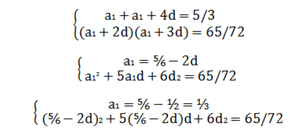
25/36-(10/3)d+4d^2+(25/6)d-10d^2+6d^2=65/72<=> (5/6)d=15/72 <=> d=1/4
4. Так как Sn=(2a1+(n-1)d)/2*n , то S17=(2/3+16/4)/2*17=(1/3+2)*17=5(2/3)+34=39(2/3) .
Ответ: S17=39(2/3).
4. Так как Sn=(2a1+(n-1)d)/2*n , то S17=(2/3+16/4)/2*17=(1/3+2)*17=5(2/3)+34=39(2/3) .
Ответ: S17=39(2/3).