Задание
Развернуть задание
Через точку O пересечения диагоналей квадрата, сторона которого равна a, проведена прямая OK, перпендикулярная к плоскости квадрата. Найдите расстояние от точки K до вершин квадрата, если OK = b.
Развернуть задание
Новое решение
Решение
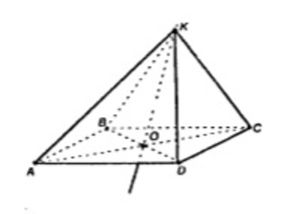
∆KOA = ∆KOB = ∆KOC = ∆KOD по двум катетам (KO ⊥ OA, KO ⊥ OB, KO ⊥ OC, KO ⊥ OD –по определению, OB = OA = OC = OD). Значит KA = KB = KC = KD
KB^2 = OK^2 + OB^2 значит KB^2 = b^2 + OB^2
BD = a√2, OB = BD/2
BD = a√2 / 2
OB^2 = a^2 / 2 => KB^2 = b^2 + a^2/2
KB = √(b^2 + a^2)
KB^2 = OK^2 + OB^2 значит KB^2 = b^2 + OB^2
BD = a√2, OB = BD/2
BD = a√2 / 2
OB^2 = a^2 / 2 => KB^2 = b^2 + a^2/2
KB = √(b^2 + a^2)

∆KOA = ∆KOB = ∆KOC = ∆KOD по двум катетам (KO ⊥ OA, KO ⊥ OB, KO ⊥ OC, KO ⊥ OD –по определению, OB = OA = OC = OD). Значит KA = KB = KC = KD
KB^2 = OK^2 + OB^2 значит KB^2 = b^2 + OB^2
BD = a√2, OB = BD/2
BD = a√2 / 2
OB^2 = a^2 / 2 => KB^2 = b^2 + a^2/2
KB = √(b^2 + a^2)
KB^2 = OK^2 + OB^2 значит KB^2 = b^2 + OB^2
BD = a√2, OB = BD/2
BD = a√2 / 2
OB^2 = a^2 / 2 => KB^2 = b^2 + a^2/2
KB = √(b^2 + a^2)