Задание
Развернуть задание
В треугольнике ABC дано: ∠C = 90˚, AC = 6 см, BC = 8 см, CM – медиана.
Через вершину C проведена прямая CK, перпендикулярная к плоскости треугольника ABC, причем CK = 12 см. Найдите KM.
Через вершину C проведена прямая CK, перпендикулярная к плоскости треугольника ABC, причем CK = 12 см. Найдите KM.
Развернуть задание
Новое решение
Решение
- Предыдущее
- Следующее
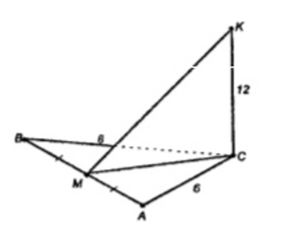
Рассмотрим ∆ABC. По условию, он прямоугольный. Найдём по т. Пифагора АВ:
AB^2=AC^2+BC^2
AB = 10 см
По свойству медианы в прямоугольном треугольнике (медиана, проведённая из вершины прямого угла, равна половине гипотенузы), СМ = 5 см.
Рассмотрим ∆КМC, он прямоугольный, по т. Пифагора
КМ^2=СМ^2+КС^2
КМ^2=25+144=169
КМ=13 см
Ответ: 13 см
AB^2=AC^2+BC^2
AB = 10 см
По свойству медианы в прямоугольном треугольнике (медиана, проведённая из вершины прямого угла, равна половине гипотенузы), СМ = 5 см.
Рассмотрим ∆КМC, он прямоугольный, по т. Пифагора
КМ^2=СМ^2+КС^2
КМ^2=25+144=169
КМ=13 см
Ответ: 13 см

Рассмотрим ∆ABC. По условию, он прямоугольный. Найдём по т. Пифагора АВ:
AB^2=AC^2+BC^2
AB = 10 см
По свойству медианы в прямоугольном треугольнике (медиана, проведённая из вершины прямого угла, равна половине гипотенузы), СМ = 5 см.
Рассмотрим ∆КМC, он прямоугольный, по т. Пифагора
КМ^2=СМ^2+КС^2
КМ^2=25+144=169
КМ=13 см
Ответ: 13 см
AB^2=AC^2+BC^2
AB = 10 см
По свойству медианы в прямоугольном треугольнике (медиана, проведённая из вершины прямого угла, равна половине гипотенузы), СМ = 5 см.
Рассмотрим ∆КМC, он прямоугольный, по т. Пифагора
КМ^2=СМ^2+КС^2
КМ^2=25+144=169
КМ=13 см
Ответ: 13 см