Задание
Развернуть задание
Прямая CD перпендикулярна к плоскости правильного треугольника ABC. Через центр O этого треугольника проведена прямая OK, параллельная прямой CD. Известно, что AB =16√3 см, OK = 12 см, CD = 16 см. Найдите расстояния от точек D и K до вершин A и B треугольника.
Развернуть задание
Новое решение
Решение
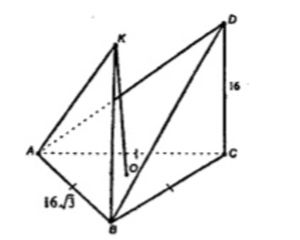
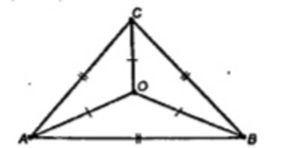
Рассмотрим ∆DAC и ∆DAB.
из условия - DC ⊥ CA, DC ⊥ CB.
AC = BC, а значит ∆DAC = ∆DСB => DA = DB
DA = DB = √(16^2 + (16√3)^2) = √(16^2 * (1 + 3)) = 32 см
OA = OB = OC = R, где R – радиус описанной окружности.
2R = a/sin α (из теоремы косинусов)
R = AB/(2 * sin ∠C) = 16√3 / (2 * sin 60˚) = 16√3 / √3 = 16 см
OA = OB = OC = R = 16 см
∆KOA = ∆KOB (равенство двух катетов) => AK = KB.
AK = KB = √(OA^2 + OK^2) = 20 см
Ответ: DA = DB = 32 см, AK = KB = 20 см
из условия - DC ⊥ CA, DC ⊥ CB.
AC = BC, а значит ∆DAC = ∆DСB => DA = DB
DA = DB = √(16^2 + (16√3)^2) = √(16^2 * (1 + 3)) = 32 см
OA = OB = OC = R, где R – радиус описанной окружности.
2R = a/sin α (из теоремы косинусов)
R = AB/(2 * sin ∠C) = 16√3 / (2 * sin 60˚) = 16√3 / √3 = 16 см
OA = OB = OC = R = 16 см
∆KOA = ∆KOB (равенство двух катетов) => AK = KB.
AK = KB = √(OA^2 + OK^2) = 20 см
Ответ: DA = DB = 32 см, AK = KB = 20 см


Рассмотрим ∆DAC и ∆DAB.
из условия - DC ⊥ CA, DC ⊥ CB.
AC = BC, а значит ∆DAC = ∆DСB => DA = DB
DA = DB = √(16^2 + (16√3)^2) = √(16^2 * (1 + 3)) = 32 см
OA = OB = OC = R, где R – радиус описанной окружности.
2R = a/sin α (из теоремы косинусов)
R = AB/(2 * sin ∠C) = 16√3 / (2 * sin 60˚) = 16√3 / √3 = 16 см
OA = OB = OC = R = 16 см
∆KOA = ∆KOB (равенство двух катетов) => AK = KB.
AK = KB = √(OA^2 + OK^2) = 20 см
Ответ: DA = DB = 32 см, AK = KB = 20 см
из условия - DC ⊥ CA, DC ⊥ CB.
AC = BC, а значит ∆DAC = ∆DСB => DA = DB
DA = DB = √(16^2 + (16√3)^2) = √(16^2 * (1 + 3)) = 32 см
OA = OB = OC = R, где R – радиус описанной окружности.
2R = a/sin α (из теоремы косинусов)
R = AB/(2 * sin ∠C) = 16√3 / (2 * sin 60˚) = 16√3 / √3 = 16 см
OA = OB = OC = R = 16 см
∆KOA = ∆KOB (равенство двух катетов) => AK = KB.
AK = KB = √(OA^2 + OK^2) = 20 см
Ответ: DA = DB = 32 см, AK = KB = 20 см