Решения
Анастасия


07-12-2016 13:55

0
Задания
Задание
Ира
28-11-2016
19:15
Школа

Геометрия

10 класс


10
1
0
0

Перпендикулярность прямой и плоскости, признаки и свойства

Доказать равенство прямых.

Развернуть задание
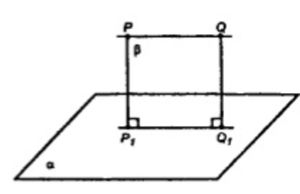
Прямая PQ параллельна плоскости α. Через точки P и Q проведены прямые, перпендикулярные к плоскости α, которые пересекают эту плоскость соответственно в точках P1 и Q1. Докажите, что PQ = P1Q1.
Сергей Геннадиевич
Новый коммент
24-07-2017 17:41:17
Алиса
Судя по таблице удельной теплоёмкости, это может быть цинк.
22-11-2016 12:57:23
Анастасия
Дмитрий Да, перевод обязателен.
21-11-2016 19:00:39
Дмитрий
1) –Обязательно ли переводить массу мяча в СИ?
21-11-2016 18:51:12
Рогова Дарья
Условие смущает. Ладно, пусть время будет отрицательным, наблюдать можно с любого момента, но не ясно, каким моментам времени соответствуют моменты изменения скорости. Можно предположить, что первый пик где-то в районе -1,5 с, но так ли это?.. Третий пик вообще без координатной сетки не определишь. И еще: график чего именно надо построить? МОДУЛЯ скорости или ПРОЕКЦИИ скорости?
3-11-2016 00:11:19
Андрей Анатольевич
Почему картика в блоке так размыта? А при просмотре в правой части (крупно) все выглядит гораздо лучше. Как то плохо пережимается картинка.
2-11-2016 15:29:02
Андрей Анатольевич
t = 20ºC или 200 С ?
31-10-2016 20:21:46
Эдуард Блохин
Интересное задание. Пригодится.
27-10-2016 14:34:02
Развернуть задание
Новое решение
Сложность
4 3 2 1
Решение
Анастасия
7-12-2016 13:55:02
0
Дано:
PQ || α, PP1, QQ1 ⊥ α.

PP1 || QQ1, как перпендикулярные одной плоскости. Значит PP1 и QQ1 принадлежат одной плоскости. Назовем ее β.
Пусть P1Q1 || PQ. Отсюда вытекает, что PQQ1P1 – параллелограмм, а значит PQ = P1Q1.
Sh Polina
ValeryL Да, можно. Но не во всех таблицах есть антрацит.
5-12-2016 12:24:15
Sh Polina
ValeryL Да, 10 миллиардов Джоулей (10 ГигаДжоулей). Ну, с учётом того, что было сожжено
2300 кг топлива – не так уж и много.
5-12-2016 12:23:52
Sh Polina
ValeryL Легко – достаточно всего лишь знать их массу и плотность. Поэтому в задаче требуется
найти обратное.
5-12-2016 12:23:26
Sh Polina
ValeryL Перед вычислениями всегда все единицы измерений нужно привести к единой системе
СИ.
5-12-2016 12:22:59
Sh Polina
ValeryL В данном случае – точно нет, потому что у бензина и керосина она одинакова.
5-12-2016 12:22:26
Sh Polina
ValeryL Смотря как изменить. Если после изменения масса водорода увеличится, а масса дров
уменьшится или останется такая же, то да, разница увеличится. Если наоборот, то
уменьшится. А если масса после изменения всё равно останется равной, то разница
останется точно такая же – в ≈ 9 раз.
5-12-2016 12:21:52
Sh Polina
ValeryL Масса одинакова, да, но удельная теплота сгорания бензина значительно больше
удельной теплоты сгорания сухих берёзовых дров, поэтому и выделится значительно
больше тепла.
5-12-2016 12:21:21
Sh Polina
ValeryL Это всего лишь немного переделанная формула плотности “p = m / V”.
5-12-2016 12:20:46
Sh Polina
ValeryL Из таблицы плотности веществ/материалов.
5-12-2016 12:20:15
Sh Polina
ValeryL Да, когда решаешь такого рода задачи, она должна быть под рукой.
5-12-2016 12:19:50
Sh Polina
ValeryL Можно и в килограммах. Для такого рода заданий так измерять удобнее.
5-12-2016 12:19:16
Sh Polina
ValeryL Из таблицы удельной теплоты сгорания веществ в воздухе.
5-12-2016 12:18:48
Sh Polina
ValeryL Да, если масса или удельная теплота сгорания равны нулю.
5-12-2016 12:18:22
Sh Polina
ValeryL Это как раз-таки и есть удельная теплота сгорания.
5-12-2016 12:15:55
ValeryL
Выходит, что каменного угля понадобилось в 2 раза меньше, чем торфа, потому что его
удельная теплота сгорания в 2 раза больше?
5-12-2016 12:14:27
ValeryL
Если бы мы сжигали не каменный уголь, а, например, древесный, то ответ бы
изменился?
5-12-2016 12:13:27
ValeryL
Откуда мы взяли массу футбольного мяча?
5-12-2016 12:12:43
ValeryL
Что такое g в формуле “E = mgh”
5-12-2016 12:11:48
ValeryL
А просто посмотреть удельную теплоту сгорания антрацита в таблице можно ж было?
5-12-2016 12:11:00
ValeryL
10^10 – это же 10 миллиардов? Многовато.
5-12-2016 12:10:20
Анастасия
7-12-2016 13:55:02
0
Дано:
PQ || α, PP1, QQ1 ⊥ α.

PP1 || QQ1, как перпендикулярные одной плоскости. Значит PP1 и QQ1 принадлежат одной плоскости. Назовем ее β.
Пусть P1Q1 || PQ. Отсюда вытекает, что PQQ1P1 – параллелограмм, а значит PQ = P1Q1.
Новость часа

Форма обратной связи