Задание
Развернуть задание
Через точки P и Q прямой PQ проведены прямые, перпендикулярные к плоскости α и пересекающие ее соответственно в точках P1 и Q1. Найдите P1Q1, если PQ = 15 см, PP1 = 21.5 см, QQ1 = 33.5 см.
Развернуть задание
Новое решение
Решение
- Предыдущее
- Следующее
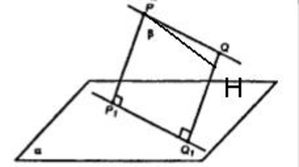
PP1 || QQ1 –отрезки перпендикулярные одной плоскости (β), следовательно они параллельны.
Плоскости α и β пересекаются на P1Q1, а значит PQQ1P1 – трапеция.
Проведём высоту QH, найдём её:
QH = 33,5 - 21,5 = 12 см
Рассмотрим ∆PQH, он прямоугольный, по т. Пифагора:
PQ^2=PH^2+QH^2
225=144+ QH^2
QH = 9 см
QH=P1Q1 = 9 см
Ответ: 9 см
Плоскости α и β пересекаются на P1Q1, а значит PQQ1P1 – трапеция.
Проведём высоту QH, найдём её:
QH = 33,5 - 21,5 = 12 см
Рассмотрим ∆PQH, он прямоугольный, по т. Пифагора:
PQ^2=PH^2+QH^2
225=144+ QH^2
QH = 9 см
QH=P1Q1 = 9 см
Ответ: 9 см

PP1 || QQ1 –отрезки перпендикулярные одной плоскости (β), следовательно они параллельны.
Плоскости α и β пересекаются на P1Q1, а значит PQQ1P1 – трапеция.
Проведём высоту QH, найдём её:
QH = 33,5 - 21,5 = 12 см
Рассмотрим ∆PQH, он прямоугольный, по т. Пифагора:
PQ^2=PH^2+QH^2
225=144+ QH^2
QH = 9 см
QH=P1Q1 = 9 см
Ответ: 9 см
Плоскости α и β пересекаются на P1Q1, а значит PQQ1P1 – трапеция.
Проведём высоту QH, найдём её:
QH = 33,5 - 21,5 = 12 см
Рассмотрим ∆PQH, он прямоугольный, по т. Пифагора:
PQ^2=PH^2+QH^2
225=144+ QH^2
QH = 9 см
QH=P1Q1 = 9 см
Ответ: 9 см