Задание
Развернуть задание
Прямая MB перпендикулярна к сторонам AB и BC треугольника ABC. Определите вид треугольника MBD, где D – произвольная точка прямой AC.
Развернуть задание
Новое решение
Решение
- Предыдущее
- Следующее
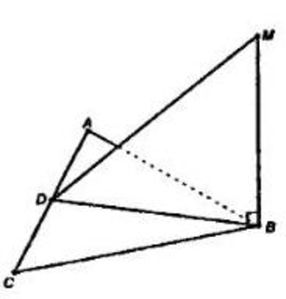
По признаку перпендикулярности прямой плоскости следует, что MB ⊥ плоскости ABC
По определению, BD ⊥ MB, отсюда следует, что угол MBD – прямой, следовательно, по определению прямоугольного треугольника, имеем, что ∆MBD – прямоугольный.
По определению, BD ⊥ MB, отсюда следует, что угол MBD – прямой, следовательно, по определению прямоугольного треугольника, имеем, что ∆MBD – прямоугольный.

По признаку перпендикулярности прямой плоскости следует, что MB ⊥ плоскости ABC
По определению, BD ⊥ MB, отсюда следует, что угол MBD – прямой, следовательно, по определению прямоугольного треугольника, имеем, что ∆MBD – прямоугольный.
По определению, BD ⊥ MB, отсюда следует, что угол MBD – прямой, следовательно, по определению прямоугольного треугольника, имеем, что ∆MBD – прямоугольный.