Задание
Развернуть задание
В треугольнике ABC сумма углов A и B = 90˚. Прямая BD перпендикулярна к плоскости ABC. Докажите, что CD ⊥ AC.
Развернуть задание
Новое решение
Решение
- Предыдущее
- Следующее
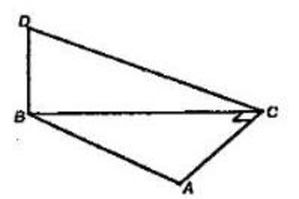
Рассмотрим ∆АВС, т.к. по условию ∠A + ∠B = 90˚, то следовательно ∠С = 90˚ и ∆АВС - прямоугольный
ВD ⊥ плоскости ∆АВС (по условию), AC ⊥ BC (как было только что установлено).
Тогда, по признаку перпендикулярности прямой и плоскости, AC ⊥ BCD.
Но DC находится в плоскости BCD. А если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, лежащей в данной плоскости, следовательно, AC ⊥ DC
ВD ⊥ плоскости ∆АВС (по условию), AC ⊥ BC (как было только что установлено).
Тогда, по признаку перпендикулярности прямой и плоскости, AC ⊥ BCD.
Но DC находится в плоскости BCD. А если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, лежащей в данной плоскости, следовательно, AC ⊥ DC

Рассмотрим ∆АВС, т.к. по условию ∠A + ∠B = 90˚, то следовательно ∠С = 90˚ и ∆АВС - прямоугольный
ВD ⊥ плоскости ∆АВС (по условию), AC ⊥ BC (как было только что установлено).
Тогда, по признаку перпендикулярности прямой и плоскости, AC ⊥ BCD.
Но DC находится в плоскости BCD. А если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, лежащей в данной плоскости, следовательно, AC ⊥ DC
ВD ⊥ плоскости ∆АВС (по условию), AC ⊥ BC (как было только что установлено).
Тогда, по признаку перпендикулярности прямой и плоскости, AC ⊥ BCD.
Но DC находится в плоскости BCD. А если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, лежащей в данной плоскости, следовательно, AC ⊥ DC