Задание
Развернуть задание
Докажите, что если одна из двух параллельных плоскостей перпендикулярна к прямой, то и другая плоскость перпендикулярна к этой прямой.
Развернуть задание
Новое решение
Решение
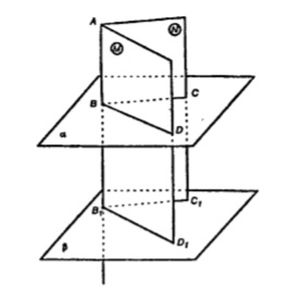
Пусть α || β, а прямая BB1 ⊥ α. Докажем, что BB1 ⊥ β.
Проведем через BB1 плоскости M и N;
BC || B1C1 и BD || B1D1.
По условию: BB1 ⊥ BC и BB1 ⊥ BD (т.к. BB1 ⊥ α).
BB1 ⊥ B1C и BB1 ⊥ B1D1
BB1 ⊥ β, т.к. B1C1 и B1D1 лежат в плоскости β
Проведем через BB1 плоскости M и N;
BC || B1C1 и BD || B1D1.
По условию: BB1 ⊥ BC и BB1 ⊥ BD (т.к. BB1 ⊥ α).
BB1 ⊥ B1C и BB1 ⊥ B1D1
BB1 ⊥ β, т.к. B1C1 и B1D1 лежат в плоскости β
