Задание
Развернуть задание
Прямая a перпендикулярна к плоскости α и перпендикулярна к прямой b, не лежащей в этой плоскости. Докажите, что b || α
Развернуть задание
Новое решение
Решение
Пусть M – точка пересечения a с α. N ∈ a.
Проведем через N прямую c || b.
В плоскости α через N проведем прямую d1.
Через N проведем прямую d || d1
a ⊥ d1, d1 || d => a ⊥ d
a ⊥ β (Через A проходит единственная плоскость β, перпендикулярная к a)
α, β ⊥ a = α || β.
b || c, c лежит в β, α || β => b || β => b || α
Проведем через N прямую c || b.
В плоскости α через N проведем прямую d1.
Через N проведем прямую d || d1
a ⊥ d1, d1 || d => a ⊥ d
a ⊥ β (Через A проходит единственная плоскость β, перпендикулярная к a)
α, β ⊥ a = α || β.
b || c, c лежит в β, α || β => b || β => b || α
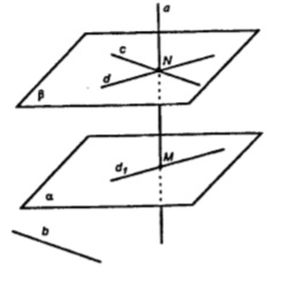
Пусть M – точка пересечения a с α. N ∈ a.
Проведем через N прямую c || b.
В плоскости α через N проведем прямую d1.
Через N проведем прямую d || d1
a ⊥ d1, d1 || d => a ⊥ d
a ⊥ β (Через A проходит единственная плоскость β, перпендикулярная к a)
α, β ⊥ a = α || β.
b || c, c лежит в β, α || β => b || β => b || α
Проведем через N прямую c || b.
В плоскости α через N проведем прямую d1.
Через N проведем прямую d || d1
a ⊥ d1, d1 || d => a ⊥ d
a ⊥ β (Через A проходит единственная плоскость β, перпендикулярная к a)
α, β ⊥ a = α || β.
b || c, c лежит в β, α || β => b || β => b || α
