Задание
Развернуть задание
Докажите, что если точка X равноудалена от концов данного отрезка AB, то она лежит в плоскости, проходящей через середину отрезка AB и перпендикулярной к прямой AB.
Развернуть задание
Новое решение
Решение
- Предыдущее
- Следующее
AX = BX
OA =OB
В каждой плоскости, проходящей через AB и некоторую xn, xn будет серединным перпендикуляром к AB, то есть равноудаленный от A и B
OA =OB
В каждой плоскости, проходящей через AB и некоторую xn, xn будет серединным перпендикуляром к AB, то есть равноудаленный от A и B
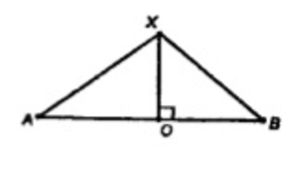
AX = BX
OA =OB
В каждой плоскости, проходящей через AB и некоторую xn, xn будет серединным перпендикуляром к AB, то есть равноудаленный от A и B
OA =OB
В каждой плоскости, проходящей через AB и некоторую xn, xn будет серединным перпендикуляром к AB, то есть равноудаленный от A и B
