Задание
Развернуть задание
Докажите, что через каждую из двух взаимно перпендикулярных скрещивающихся прямых проходит плоскость, перпендикулярная к другой прямой.
Развернуть задание
Новое решение
Решение
Пусть скрещивающиеся прямые a и b лежат в параллельных плоскостях.
Проведем через b плоскость β, β || a. Проведем AA1 ⊥ β и BB1 ⊥ β
A1B1 || AB
AB || A1B1 и AB ⊥ b, отсюда A1B1 ⊥ b
Из точки C1 проведем C1C ⊥ β. Она пересечет AB в точке C.
Значит b ⊥ C1C
b ⊥ A1B1, b ⊥ C1C и A1b1 ∩ C1C => b ⊥ A1ABB1, то через a проходит плоскость перпендикулярная к b.
Проведем через b плоскость β, β || a. Проведем AA1 ⊥ β и BB1 ⊥ β
A1B1 || AB
AB || A1B1 и AB ⊥ b, отсюда A1B1 ⊥ b
Из точки C1 проведем C1C ⊥ β. Она пересечет AB в точке C.
Значит b ⊥ C1C
b ⊥ A1B1, b ⊥ C1C и A1b1 ∩ C1C => b ⊥ A1ABB1, то через a проходит плоскость перпендикулярная к b.
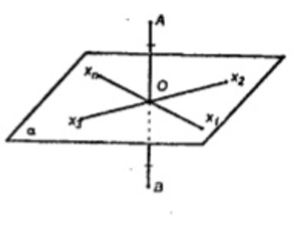
Пусть скрещивающиеся прямые a и b лежат в параллельных плоскостях.
Проведем через b плоскость β, β || a. Проведем AA1 ⊥ β и BB1 ⊥ β
A1B1 || AB
AB || A1B1 и AB ⊥ b, отсюда A1B1 ⊥ b
Из точки C1 проведем C1C ⊥ β. Она пересечет AB в точке C.
Значит b ⊥ C1C
b ⊥ A1B1, b ⊥ C1C и A1b1 ∩ C1C => b ⊥ A1ABB1, то через a проходит плоскость перпендикулярная к b.
Проведем через b плоскость β, β || a. Проведем AA1 ⊥ β и BB1 ⊥ β
A1B1 || AB
AB || A1B1 и AB ⊥ b, отсюда A1B1 ⊥ b
Из точки C1 проведем C1C ⊥ β. Она пересечет AB в точке C.
Значит b ⊥ C1C
b ⊥ A1B1, b ⊥ C1C и A1b1 ∩ C1C => b ⊥ A1ABB1, то через a проходит плоскость перпендикулярная к b.
