Задание
Развернуть задание
Из точки M проведен перпендикуляр MB к плоскости прямоугольника ABCD. Докажите, что треугольники AMD и MCD – прямоугольные.
Развернуть задание
Новое решение
Решение
- Предыдущее
- Следующее
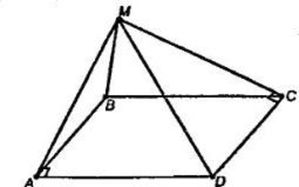
AD ⊥ AB (так как ABCD – прямоугольник), AD ⊥ MB (т.к. МВ ⊥ плоскости прямоугольника), то по т. о 3х перпендикулярах (Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и самой наклонной) ∠MAD = 90˚.
MB ⊥ DC MB (т.к. МВ ⊥ плоскости прямоугольника), BC ⊥ CD (так как ABCD – прямоугольник), снова используем теорему о трёх перпендикулярах и получаем, что ∠MCD = 90˚.
MB ⊥ DC MB (т.к. МВ ⊥ плоскости прямоугольника), BC ⊥ CD (так как ABCD – прямоугольник), снова используем теорему о трёх перпендикулярах и получаем, что ∠MCD = 90˚.

AD ⊥ AB (так как ABCD – прямоугольник), AD ⊥ MB (т.к. МВ ⊥ плоскости прямоугольника), то по т. о 3х перпендикулярах (Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и самой наклонной) ∠MAD = 90˚.
MB ⊥ DC MB (т.к. МВ ⊥ плоскости прямоугольника), BC ⊥ CD (так как ABCD – прямоугольник), снова используем теорему о трёх перпендикулярах и получаем, что ∠MCD = 90˚.
MB ⊥ DC MB (т.к. МВ ⊥ плоскости прямоугольника), BC ⊥ CD (так как ABCD – прямоугольник), снова используем теорему о трёх перпендикулярах и получаем, что ∠MCD = 90˚.