Задание
Развернуть задание
Отрезок AD перпендикулярен к плоскости равнобедренного треугольника ABC. Известно,
что AB = AC = 5 см, BC = 6 см, AD = 12 см. Найдите расстояние от концов отрезка AD до прямой BC.
что AB = AC = 5 см, BC = 6 см, AD = 12 см. Найдите расстояние от концов отрезка AD до прямой BC.
Развернуть задание
Новое решение
Решение
- Предыдущее
- Следующее
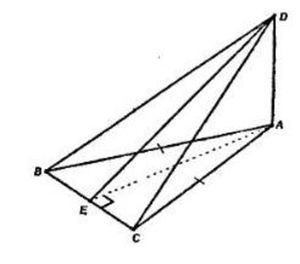
Рассмотрим ∆АВС:
Расстояние от AD до ВС – высота АЕ. Найдём ее, рассмотрев ∆АСЕ, он прямоугольный, тогда по т. Пифагора найдём АЕ:
АС^2 = EC^2 + AE^2
AC = 5 см (по условию), EC = ½*ВС = 3 см (т.к. ∆ АВС – равнобедренный, то высота, проведённая к основанию, является также медианой)
25 = АЕ^2 + 9
АЕ = 4 см
BC ⊥ AE, BC ⊥ DA, то по теореме о трех перпендикулярах получаем BC ⊥ DE
Рассмотрим ∆DCE, он прямоугольный
DC^2 = DE^2+EC^2
Из ∆АDС DC=sqrt(25+144) = 13 см
Получим:
169 = DE^2+9
DE^2 = 160
DE = 4*sqrt(10)
Ответ: АЕ = 4 см, DE = 4*sqrt(10)
Расстояние от AD до ВС – высота АЕ. Найдём ее, рассмотрев ∆АСЕ, он прямоугольный, тогда по т. Пифагора найдём АЕ:
АС^2 = EC^2 + AE^2
AC = 5 см (по условию), EC = ½*ВС = 3 см (т.к. ∆ АВС – равнобедренный, то высота, проведённая к основанию, является также медианой)
25 = АЕ^2 + 9
АЕ = 4 см
BC ⊥ AE, BC ⊥ DA, то по теореме о трех перпендикулярах получаем BC ⊥ DE
Рассмотрим ∆DCE, он прямоугольный
DC^2 = DE^2+EC^2
Из ∆АDС DC=sqrt(25+144) = 13 см
Получим:
169 = DE^2+9
DE^2 = 160
DE = 4*sqrt(10)
Ответ: АЕ = 4 см, DE = 4*sqrt(10)

Рассмотрим ∆АВС:
Расстояние от AD до ВС – высота АЕ. Найдём ее, рассмотрев ∆АСЕ, он прямоугольный, тогда по т. Пифагора найдём АЕ:
АС^2 = EC^2 + AE^2
AC = 5 см (по условию), EC = ½*ВС = 3 см (т.к. ∆ АВС – равнобедренный, то высота, проведённая к основанию, является также медианой)
25 = АЕ^2 + 9
АЕ = 4 см
BC ⊥ AE, BC ⊥ DA, то по теореме о трех перпендикулярах получаем BC ⊥ DE
Рассмотрим ∆DCE, он прямоугольный
DC^2 = DE^2+EC^2
Из ∆АDС DC=sqrt(25+144) = 13 см
Получим:
169 = DE^2+9
DE^2 = 160
DE = 4*sqrt(10)
Ответ: АЕ = 4 см, DE = 4*sqrt(10)
Расстояние от AD до ВС – высота АЕ. Найдём ее, рассмотрев ∆АСЕ, он прямоугольный, тогда по т. Пифагора найдём АЕ:
АС^2 = EC^2 + AE^2
AC = 5 см (по условию), EC = ½*ВС = 3 см (т.к. ∆ АВС – равнобедренный, то высота, проведённая к основанию, является также медианой)
25 = АЕ^2 + 9
АЕ = 4 см
BC ⊥ AE, BC ⊥ DA, то по теореме о трех перпендикулярах получаем BC ⊥ DE
Рассмотрим ∆DCE, он прямоугольный
DC^2 = DE^2+EC^2
Из ∆АDС DC=sqrt(25+144) = 13 см
Получим:
169 = DE^2+9
DE^2 = 160
DE = 4*sqrt(10)
Ответ: АЕ = 4 см, DE = 4*sqrt(10)