Задание
Развернуть задание
Точка A лежит на радиусе данной сферы с центром в точке О и делит этот радиус в отношнении 1:2, считая от центра сферы. Через точку А проведена плоскость α так, что радиус сферы с центром в точке О, касающейся плоскости α, в 6 раз меньше радиуса данной сферы. Найдите: а) угол между прямой ОА и плоскостью α; б) отношение площади сечения данной сферы плоскостью α к площади самой сферы.
Развернуть задание
Новое решение
Решение
- Предыдущее
- Следующее
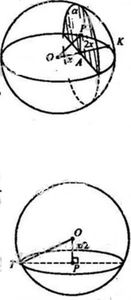
а) Пусть ОХ = х, тогда АК = 2х. Опустим из точки О перпендикуляр OP на плоскость α.
ОР = 1/6 ОК = 1/6 – 3x = x/2
∆ОРА – прямоугольный
sin OAP = OP/OA = ½, значит угол OAP=300
б) ОР = х/2, ОТ = 3х
TP^2 = OT^2 – OP^2
9x^2 – x^2/4 = 35x^2/4
TP = sqrt(35)/2*x
S1 = π(TP)^2 = 35 πx^2/4
S2 = 4 π(3x)^2 = 36 πx^2 – площадь поверхности данной сферы
S1/S2 = 35/144
ОР = 1/6 ОК = 1/6 – 3x = x/2
∆ОРА – прямоугольный
sin OAP = OP/OA = ½, значит угол OAP=300
б) ОР = х/2, ОТ = 3х
TP^2 = OT^2 – OP^2
9x^2 – x^2/4 = 35x^2/4
TP = sqrt(35)/2*x
S1 = π(TP)^2 = 35 πx^2/4
S2 = 4 π(3x)^2 = 36 πx^2 – площадь поверхности данной сферы
S1/S2 = 35/144

а) Пусть ОХ = х, тогда АК = 2х. Опустим из точки О перпендикуляр OP на плоскость α.
ОР = 1/6 ОК = 1/6 – 3x = x/2
∆ОРА – прямоугольный
sin OAP = OP/OA = ½, значит угол OAP=300
б) ОР = х/2, ОТ = 3х
TP^2 = OT^2 – OP^2
9x^2 – x^2/4 = 35x^2/4
TP = sqrt(35)/2*x
S1 = π(TP)^2 = 35 πx^2/4
S2 = 4 π(3x)^2 = 36 πx^2 – площадь поверхности данной сферы
S1/S2 = 35/144
ОР = 1/6 ОК = 1/6 – 3x = x/2
∆ОРА – прямоугольный
sin OAP = OP/OA = ½, значит угол OAP=300
б) ОР = х/2, ОТ = 3х
TP^2 = OT^2 – OP^2
9x^2 – x^2/4 = 35x^2/4
TP = sqrt(35)/2*x
S1 = π(TP)^2 = 35 πx^2/4
S2 = 4 π(3x)^2 = 36 πx^2 – площадь поверхности данной сферы
S1/S2 = 35/144