Задание
Развернуть задание
Два прямоугольника лежат в различных плоскостях и имеют общую сторону. Докажите, что все вершины данных прямоугольников лежат на одной сфере.
Развернуть задание
Новое решение
Решение
Пусть l прямая препендикулярна плоскости ABCD(прямоугольник по условию) и проходит через точку пересечения диагоналей => PA=PB=PC=PD.
Пусть OK⊥AB, AB перпендикулярна плоскости KOP. Т.к. AB находится в плоскости ABEF, то плоскости KOP и ABEF взаимно перпендикулярны.
Прямая m принадлежит плоскости KOP то QA=QB=QE=QF.
Точка S пересечение прямых m и l. Значит она равноудалена от вершин плоскости ABCD и вершин плоскости ABEF
△SAO=△SBO (по 2-м катетам)=> SA=SB. Аналогично △SEO_1=△SBO_1 =>SЕ=SB значит SA=SB=SE=SC=SD=SF => точка S- центр сферы проходящей через вершины A,B,C,D,E,F. ч.т.д.
Пусть OK⊥AB, AB перпендикулярна плоскости KOP. Т.к. AB находится в плоскости ABEF, то плоскости KOP и ABEF взаимно перпендикулярны.
Прямая m принадлежит плоскости KOP то QA=QB=QE=QF.
Точка S пересечение прямых m и l. Значит она равноудалена от вершин плоскости ABCD и вершин плоскости ABEF
△SAO=△SBO (по 2-м катетам)=> SA=SB. Аналогично △SEO_1=△SBO_1 =>SЕ=SB значит SA=SB=SE=SC=SD=SF => точка S- центр сферы проходящей через вершины A,B,C,D,E,F. ч.т.д.
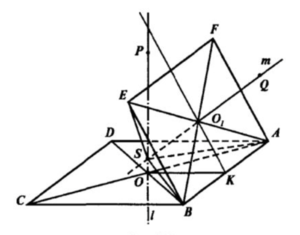
Пусть l прямая препендикулярна плоскости ABCD(прямоугольник по условию) и проходит через точку пересечения диагоналей => PA=PB=PC=PD.
Пусть OK⊥AB, AB перпендикулярна плоскости KOP. Т.к. AB находится в плоскости ABEF, то плоскости KOP и ABEF взаимно перпендикулярны.
Прямая m принадлежит плоскости KOP то QA=QB=QE=QF.
Точка S пересечение прямых m и l. Значит она равноудалена от вершин плоскости ABCD и вершин плоскости ABEF
△SAO=△SBO (по 2-м катетам)=> SA=SB. Аналогично △SEO_1=△SBO_1 =>SЕ=SB значит SA=SB=SE=SC=SD=SF => точка S- центр сферы проходящей через вершины A,B,C,D,E,F. ч.т.д.
Пусть OK⊥AB, AB перпендикулярна плоскости KOP. Т.к. AB находится в плоскости ABEF, то плоскости KOP и ABEF взаимно перпендикулярны.
Прямая m принадлежит плоскости KOP то QA=QB=QE=QF.
Точка S пересечение прямых m и l. Значит она равноудалена от вершин плоскости ABCD и вершин плоскости ABEF
△SAO=△SBO (по 2-м катетам)=> SA=SB. Аналогично △SEO_1=△SBO_1 =>SЕ=SB значит SA=SB=SE=SC=SD=SF => точка S- центр сферы проходящей через вершины A,B,C,D,E,F. ч.т.д.
