Задание
Развернуть задание
Расстояние между центрами двух равных сфер меньше их диаметра. а) Докажите, что пересечением этих сфер является окружность. б) Найдите радиус этой окружности, если радиусы сфер равны R, а расстояние между их центрами равно 1,6 R.
Развернуть задание
Новое решение
Решение
a) Построим 3-х мерную систему координат. Тогда урвнение первой сферы с центром в начале кооринат имеет вид: x^2+y^2+z^2=r^2, а урвнение другой сферы с центром в точке О_1 имеет вид: x^2+(y-d)^2+z^2=r^2.
Решим систему из этих 2-х уравнений, отнимим из 1-ого урвнения 2-е. Получим x^2+y^2+z^2-x^2-(y-d)^2-z^2=r^2-r^2 ⇔ y^2-y^2+2yd-d^2=0 ⇔d(2y-d)=0 т.к. d>0 то 2y=d или у=d/2
d<2r по условию, значит у<r т.е. есть некоторая плоскость, которая перпендикулярна оси OY и пересекает сферу, а при пересечении сферы плоскостью в сечении получим окружность ч.т.д..
б) Т.к. y=d/2 то подставим это значение в уравнение сферы: x^2+d^2/4+z^2=r^2.
d=1,6r по условию, значит x^2+(1,6r)^2/4+z^2=r^2 ⇔ x^2+z^2=r^2-2,56r^2/4 ⇔ x^2+z^2=r^2-0,64r^2 ⇔ x^2+z^2=0,36r^2. Получили уравнение окружности перпендикулярной оси OY и параллельной к окружности, которая пересекает эти 2 сферы. Pадиус этой окружности √0,36r^2=0,6r
Ответ:0,6r
Решим систему из этих 2-х уравнений, отнимим из 1-ого урвнения 2-е. Получим x^2+y^2+z^2-x^2-(y-d)^2-z^2=r^2-r^2 ⇔ y^2-y^2+2yd-d^2=0 ⇔d(2y-d)=0 т.к. d>0 то 2y=d или у=d/2
d<2r по условию, значит у<r т.е. есть некоторая плоскость, которая перпендикулярна оси OY и пересекает сферу, а при пересечении сферы плоскостью в сечении получим окружность ч.т.д..
б) Т.к. y=d/2 то подставим это значение в уравнение сферы: x^2+d^2/4+z^2=r^2.
d=1,6r по условию, значит x^2+(1,6r)^2/4+z^2=r^2 ⇔ x^2+z^2=r^2-2,56r^2/4 ⇔ x^2+z^2=r^2-0,64r^2 ⇔ x^2+z^2=0,36r^2. Получили уравнение окружности перпендикулярной оси OY и параллельной к окружности, которая пересекает эти 2 сферы. Pадиус этой окружности √0,36r^2=0,6r
Ответ:0,6r
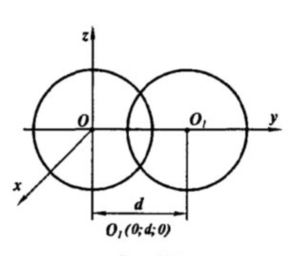
a) Построим 3-х мерную систему координат. Тогда урвнение первой сферы с центром в начале кооринат имеет вид: x^2+y^2+z^2=r^2, а урвнение другой сферы с центром в точке О_1 имеет вид: x^2+(y-d)^2+z^2=r^2.
Решим систему из этих 2-х уравнений, отнимим из 1-ого урвнения 2-е. Получим x^2+y^2+z^2-x^2-(y-d)^2-z^2=r^2-r^2 ⇔ y^2-y^2+2yd-d^2=0 ⇔d(2y-d)=0 т.к. d>0 то 2y=d или у=d/2
d<2r по условию, значит у<r т.е. есть некоторая плоскость, которая перпендикулярна оси OY и пересекает сферу, а при пересечении сферы плоскостью в сечении получим окружность ч.т.д..
б) Т.к. y=d/2 то подставим это значение в уравнение сферы: x^2+d^2/4+z^2=r^2.
d=1,6r по условию, значит x^2+(1,6r)^2/4+z^2=r^2 ⇔ x^2+z^2=r^2-2,56r^2/4 ⇔ x^2+z^2=r^2-0,64r^2 ⇔ x^2+z^2=0,36r^2. Получили уравнение окружности перпендикулярной оси OY и параллельной к окружности, которая пересекает эти 2 сферы. Pадиус этой окружности √0,36r^2=0,6r
Ответ:0,6r
Решим систему из этих 2-х уравнений, отнимим из 1-ого урвнения 2-е. Получим x^2+y^2+z^2-x^2-(y-d)^2-z^2=r^2-r^2 ⇔ y^2-y^2+2yd-d^2=0 ⇔d(2y-d)=0 т.к. d>0 то 2y=d или у=d/2
d<2r по условию, значит у<r т.е. есть некоторая плоскость, которая перпендикулярна оси OY и пересекает сферу, а при пересечении сферы плоскостью в сечении получим окружность ч.т.д..
б) Т.к. y=d/2 то подставим это значение в уравнение сферы: x^2+d^2/4+z^2=r^2.
d=1,6r по условию, значит x^2+(1,6r)^2/4+z^2=r^2 ⇔ x^2+z^2=r^2-2,56r^2/4 ⇔ x^2+z^2=r^2-0,64r^2 ⇔ x^2+z^2=0,36r^2. Получили уравнение окружности перпендикулярной оси OY и параллельной к окружности, которая пересекает эти 2 сферы. Pадиус этой окружности √0,36r^2=0,6r
Ответ:0,6r
