Задание
Развернуть задание
Точки А, В, С и D лежат на сфере радиуса R, причем ∠ADB= ∠BDC=∠CDA = 2φ, AD = BD = CD. Найдите: а) АВ и AD; б) площадь сечения сферы плоскостью ABC.
Развернуть задание
Новое решение
Решение
а)
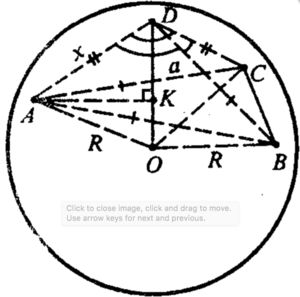
1) Пусть DK перпендикулярен плоскости АВС △DKA=△DKB=△DКC (по катету и гипотенузе). Значит KA=KB=КC=r-радиус описанной окружности ококо △ABC.
2) Пусть OT перпендикулярен плоскости АВС △OTA=△OTB=△OTC (по 2м катетам). Значит TA=TB=TC=r-радиус описанной окружности ококо △ABC.
3) Значит точки Т и K совпадают => DO перпендикулярен плоскости АВС.
4) △ABD=△BCD=△ACD (по 2м сторонам и углу между ними). Значит AВ=BС=AC => △ABC равносторонний.
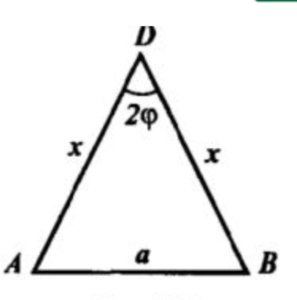
5)Пусть AB=a, AD=DB=x. ∠DAB=(180^o-2φ)/2=90^o-φ.
a/sin2φ=x/sin(90^o-φ) по теор. синусов. a/(2sinφcosφ)=x/cosφ ⇔ a*cosφ=2x*sinφcosφ ⇔ a=2x*sinφ
a/sin60^o=2r по теор. cинусов. a=√3r ⇔ r=2x*sinφ/√3
6) DK=√(AD^2-AK^2)=√(x^2-r^2) по теор. Пифагора
ОК=√(AО^2-AK^2)=√(R^2-r^2) по теор. Пифагора
7) DK+KO=R или √(x^2-r^2)+√(R^2-r^2)=R ⇔ x^2-r^2+R^2-r^2+2√((x^2-r^2)(R^2-r^2))=R^2 ⇔ 2√((x^2-r^2)(R^2-r^2))=2r^2-x^2 ⇔ 4(x^2-r^2)(R^2-r^2)=4r^4+x^4-4(rx)^2 ⇔ 4(xR)^2-4(xr)^2-4(rR)^2+4r^4=4r^4+x^4-4(rx)^2 ⇔ x^4-4(xR)^2+4(rR)^2=0 ⇔ x^4-4(xR)^2+16R^2*x^2*sin^2φ/3=0 ⇔ x^2(x^2-4R^2+16R^2*sin^2φ/3)=0 x>0, значит x^2=4R^2-16R^2*sin^2φ/3 ⇔ x=AD=√(4R^2(1-4/3*sin^2φ))=2R√(1-4/3*sin^2φ)=2R√((3-4*sin^2φ)/3)
8) a=AB=4Rsinφ√((3-4*sin^2φ)/3)
Ответ: AB=4Rsinφ√((3-4*sin^2φ)/3); AD=2R√((3-4*sin^2φ)/3)
б)
Сечение сферы и плоскости ABC это окружность r-радиус этой окружности.
r=2x*sinφ/√3=4R√(3-4*sin^2φ)/√3*sinφ/√3=4/3*Rsinφ√(3-4*sin^2φ)
S_сеч=πr^2=π*16/9*R^2sin^2φ(3-4*sin^2φ)
Ответ: S_сеч=π*16/9*R^2sin^2φ(3-4*sin^2φ)
1) Пусть DK перпендикулярен плоскости АВС △DKA=△DKB=△DКC (по катету и гипотенузе). Значит KA=KB=КC=r-радиус описанной окружности ококо △ABC.
2) Пусть OT перпендикулярен плоскости АВС △OTA=△OTB=△OTC (по 2м катетам). Значит TA=TB=TC=r-радиус описанной окружности ококо △ABC.
3) Значит точки Т и K совпадают => DO перпендикулярен плоскости АВС.
4) △ABD=△BCD=△ACD (по 2м сторонам и углу между ними). Значит AВ=BС=AC => △ABC равносторонний.
5)Пусть AB=a, AD=DB=x. ∠DAB=(180^o-2φ)/2=90^o-φ.
a/sin2φ=x/sin(90^o-φ) по теор. синусов. a/(2sinφcosφ)=x/cosφ ⇔ a*cosφ=2x*sinφcosφ ⇔ a=2x*sinφ
a/sin60^o=2r по теор. cинусов. a=√3r ⇔ r=2x*sinφ/√3
6) DK=√(AD^2-AK^2)=√(x^2-r^2) по теор. Пифагора
ОК=√(AО^2-AK^2)=√(R^2-r^2) по теор. Пифагора
7) DK+KO=R или √(x^2-r^2)+√(R^2-r^2)=R ⇔ x^2-r^2+R^2-r^2+2√((x^2-r^2)(R^2-r^2))=R^2 ⇔ 2√((x^2-r^2)(R^2-r^2))=2r^2-x^2 ⇔ 4(x^2-r^2)(R^2-r^2)=4r^4+x^4-4(rx)^2 ⇔ 4(xR)^2-4(xr)^2-4(rR)^2+4r^4=4r^4+x^4-4(rx)^2 ⇔ x^4-4(xR)^2+4(rR)^2=0 ⇔ x^4-4(xR)^2+16R^2*x^2*sin^2φ/3=0 ⇔ x^2(x^2-4R^2+16R^2*sin^2φ/3)=0 x>0, значит x^2=4R^2-16R^2*sin^2φ/3 ⇔ x=AD=√(4R^2(1-4/3*sin^2φ))=2R√(1-4/3*sin^2φ)=2R√((3-4*sin^2φ)/3)
8) a=AB=4Rsinφ√((3-4*sin^2φ)/3)
Ответ: AB=4Rsinφ√((3-4*sin^2φ)/3); AD=2R√((3-4*sin^2φ)/3)
б)
Сечение сферы и плоскости ABC это окружность r-радиус этой окружности.
r=2x*sinφ/√3=4R√(3-4*sin^2φ)/√3*sinφ/√3=4/3*Rsinφ√(3-4*sin^2φ)
S_сеч=πr^2=π*16/9*R^2sin^2φ(3-4*sin^2φ)
Ответ: S_сеч=π*16/9*R^2sin^2φ(3-4*sin^2φ)
а)
1) Пусть DK перпендикулярен плоскости АВС △DKA=△DKB=△DКC (по катету и гипотенузе). Значит KA=KB=КC=r-радиус описанной окружности ококо △ABC.
2) Пусть OT перпендикулярен плоскости АВС △OTA=△OTB=△OTC (по 2м катетам). Значит TA=TB=TC=r-радиус описанной окружности ококо △ABC.
3) Значит точки Т и K совпадают => DO перпендикулярен плоскости АВС.
4) △ABD=△BCD=△ACD (по 2м сторонам и углу между ними). Значит AВ=BС=AC => △ABC равносторонний.
5)Пусть AB=a, AD=DB=x. ∠DAB=(180^o-2φ)/2=90^o-φ.
a/sin2φ=x/sin(90^o-φ) по теор. синусов. a/(2sinφcosφ)=x/cosφ ⇔ a*cosφ=2x*sinφcosφ ⇔ a=2x*sinφ
a/sin60^o=2r по теор. cинусов. a=√3r ⇔ r=2x*sinφ/√3
6) DK=√(AD^2-AK^2)=√(x^2-r^2) по теор. Пифагора
ОК=√(AО^2-AK^2)=√(R^2-r^2) по теор. Пифагора
7) DK+KO=R или √(x^2-r^2)+√(R^2-r^2)=R ⇔ x^2-r^2+R^2-r^2+2√((x^2-r^2)(R^2-r^2))=R^2 ⇔ 2√((x^2-r^2)(R^2-r^2))=2r^2-x^2 ⇔ 4(x^2-r^2)(R^2-r^2)=4r^4+x^4-4(rx)^2 ⇔ 4(xR)^2-4(xr)^2-4(rR)^2+4r^4=4r^4+x^4-4(rx)^2 ⇔ x^4-4(xR)^2+4(rR)^2=0 ⇔ x^4-4(xR)^2+16R^2*x^2*sin^2φ/3=0 ⇔ x^2(x^2-4R^2+16R^2*sin^2φ/3)=0 x>0, значит x^2=4R^2-16R^2*sin^2φ/3 ⇔ x=AD=√(4R^2(1-4/3*sin^2φ))=2R√(1-4/3*sin^2φ)=2R√((3-4*sin^2φ)/3)
8) a=AB=4Rsinφ√((3-4*sin^2φ)/3)
Ответ: AB=4Rsinφ√((3-4*sin^2φ)/3); AD=2R√((3-4*sin^2φ)/3)
б)
Сечение сферы и плоскости ABC это окружность r-радиус этой окружности.
r=2x*sinφ/√3=4R√(3-4*sin^2φ)/√3*sinφ/√3=4/3*Rsinφ√(3-4*sin^2φ)
S_сеч=πr^2=π*16/9*R^2sin^2φ(3-4*sin^2φ)
Ответ: S_сеч=π*16/9*R^2sin^2φ(3-4*sin^2φ)
1) Пусть DK перпендикулярен плоскости АВС △DKA=△DKB=△DКC (по катету и гипотенузе). Значит KA=KB=КC=r-радиус описанной окружности ококо △ABC.
2) Пусть OT перпендикулярен плоскости АВС △OTA=△OTB=△OTC (по 2м катетам). Значит TA=TB=TC=r-радиус описанной окружности ококо △ABC.
3) Значит точки Т и K совпадают => DO перпендикулярен плоскости АВС.
4) △ABD=△BCD=△ACD (по 2м сторонам и углу между ними). Значит AВ=BС=AC => △ABC равносторонний.
5)Пусть AB=a, AD=DB=x. ∠DAB=(180^o-2φ)/2=90^o-φ.
a/sin2φ=x/sin(90^o-φ) по теор. синусов. a/(2sinφcosφ)=x/cosφ ⇔ a*cosφ=2x*sinφcosφ ⇔ a=2x*sinφ
a/sin60^o=2r по теор. cинусов. a=√3r ⇔ r=2x*sinφ/√3
6) DK=√(AD^2-AK^2)=√(x^2-r^2) по теор. Пифагора
ОК=√(AО^2-AK^2)=√(R^2-r^2) по теор. Пифагора
7) DK+KO=R или √(x^2-r^2)+√(R^2-r^2)=R ⇔ x^2-r^2+R^2-r^2+2√((x^2-r^2)(R^2-r^2))=R^2 ⇔ 2√((x^2-r^2)(R^2-r^2))=2r^2-x^2 ⇔ 4(x^2-r^2)(R^2-r^2)=4r^4+x^4-4(rx)^2 ⇔ 4(xR)^2-4(xr)^2-4(rR)^2+4r^4=4r^4+x^4-4(rx)^2 ⇔ x^4-4(xR)^2+4(rR)^2=0 ⇔ x^4-4(xR)^2+16R^2*x^2*sin^2φ/3=0 ⇔ x^2(x^2-4R^2+16R^2*sin^2φ/3)=0 x>0, значит x^2=4R^2-16R^2*sin^2φ/3 ⇔ x=AD=√(4R^2(1-4/3*sin^2φ))=2R√(1-4/3*sin^2φ)=2R√((3-4*sin^2φ)/3)
8) a=AB=4Rsinφ√((3-4*sin^2φ)/3)
Ответ: AB=4Rsinφ√((3-4*sin^2φ)/3); AD=2R√((3-4*sin^2φ)/3)
б)
Сечение сферы и плоскости ABC это окружность r-радиус этой окружности.
r=2x*sinφ/√3=4R√(3-4*sin^2φ)/√3*sinφ/√3=4/3*Rsinφ√(3-4*sin^2φ)
S_сеч=πr^2=π*16/9*R^2sin^2φ(3-4*sin^2φ)
Ответ: S_сеч=π*16/9*R^2sin^2φ(3-4*sin^2φ)

