Задание
Развернуть задание
Тело ограничено двумя сферами с общим центром. Докажите, что площадь его сечения плоскостью, проходящей через центры сфер, равна площади сечения плоскостью, касательной к внутренней сфере.
Развернуть задание
Новое решение
Решение
- Предыдущее
- Следующее
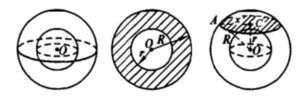
r – радиус внутренней сферы, R – внешней
Искомое сечение – кольцо
S = π(R^2 – r^2)
OC = r – перпендикулярен к плоскости в сечении
∆ACO – прямоугольный. По т. Пифагора:
х = sqrt(R^2 – r^2)
S сеч = πх^2 = π(R^2 – r^2)
Площадь кольца совпадает с площадью плоскости, касательной к внутренней сфере
Искомое сечение – кольцо
S = π(R^2 – r^2)
OC = r – перпендикулярен к плоскости в сечении
∆ACO – прямоугольный. По т. Пифагора:
х = sqrt(R^2 – r^2)
S сеч = πх^2 = π(R^2 – r^2)
Площадь кольца совпадает с площадью плоскости, касательной к внутренней сфере
