Задание
Развернуть задание
Через вершину прямого угла C равнобедренного прямоугольного треугольника ABC проведена прямая CM, перпендикулярная к его плоскости. Найдите расстояние от точки M до прямой AB, если AC = 4 см, а CM = 2√7 см.
Развернуть задание
Новое решение
Решение
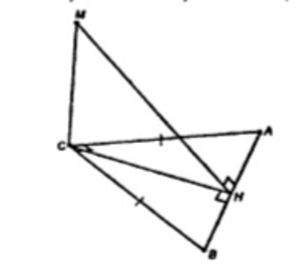
Дано: ∆ABC, AC = CB, AC = 4 см, CM = 2√7 см
CH ⊥ AB, MC ⊥ AB, то (по т. о 3х перпендикулярах) MH ⊥ AB.
p(M, AB) = MH = √(MC^2 + CH^2) , т.к. MH ⊥ AB
B ∆ABC: CH = BC * sin 45˚ = 2√2 см
MH = √(28 + 8) = 6 см
Ответ: 6 см
CH ⊥ AB, MC ⊥ AB, то (по т. о 3х перпендикулярах) MH ⊥ AB.
p(M, AB) = MH = √(MC^2 + CH^2) , т.к. MH ⊥ AB
B ∆ABC: CH = BC * sin 45˚ = 2√2 см
MH = √(28 + 8) = 6 см
Ответ: 6 см
