Решения
Sh
Polina

30-11-2016 18:46

0
Задания
Задание

Дмитрий
29-11-2016
21:43
Школа

Геометрия

10 класс


10
1
0
0

Расстояние от точки до плоскости

Решить задачу, найти расстояние от точки до плоскости

Развернуть задание
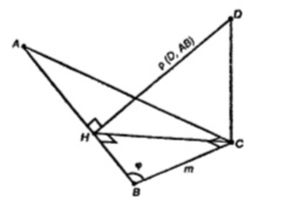
Один из катетов прямоугольного треугольника ABC равен m, а острый угол, прилежащий к этому катету, равен φ. Через вершину прямого угла C проведена прямая CD, перпендикулярная к плоскости этого треугольника CD = n. Найдите расстояние от точки D до прямой AB.
Сергей Геннадиевич
Новый коммент
24-07-2017 17:41:17
Алиса
Судя по таблице удельной теплоёмкости, это может быть цинк.
22-11-2016 12:57:23
Анастасия
Дмитрий Да, перевод обязателен.
21-11-2016 19:00:39
Дмитрий
1) –Обязательно ли переводить массу мяча в СИ?
21-11-2016 18:51:12
Рогова Дарья
Условие смущает. Ладно, пусть время будет отрицательным, наблюдать можно с любого момента, но не ясно, каким моментам времени соответствуют моменты изменения скорости. Можно предположить, что первый пик где-то в районе -1,5 с, но так ли это?.. Третий пик вообще без координатной сетки не определишь. И еще: график чего именно надо построить? МОДУЛЯ скорости или ПРОЕКЦИИ скорости?
3-11-2016 00:11:19
Андрей Анатольевич
Почему картика в блоке так размыта? А при просмотре в правой части (крупно) все выглядит гораздо лучше. Как то плохо пережимается картинка.
2-11-2016 15:29:02
Андрей Анатольевич
t = 20ºC или 200 С ?
31-10-2016 20:21:46
Эдуард Блохин
Интересное задание. Пригодится.
27-10-2016 14:34:02
Развернуть задание
Новое решение
Сложность
4 3 2 1
Решение
Sh
Polina
30-11-2016 18:46:44
0
Проведем CH ⊥ AB и DH.
DC ⊥ СН и CH ⊥ AB =>DH ⊥ AB
Из ∆ABC CH = m * sin φ.
В ∆DCH: DH = √(DC^2 + CH^2) = √(n^2 + m^2 * sin^2 φ)
Ответ: √(n^2 + m^2 * sin^2 φ)
Лолита
Влада Это мы получаем из формулы скорости: v = s/t, где v – скорость, s – пройденное
расстояние, а t – время, за которое объект прошел расстояние s.
Преобразуем это к формуле для t:
v = s/t
v * t = s
t = s/v
28-11-2016 22:17:11
Лолита
А если уже пересеклись?
28-11-2016 22:07:14
Алиса
Влада Все очень просто: раскрыли скобки в левой части, чтобы потом сложить подобные и
найти x, а в правой части пройденный поездами путь уменьшили на 30, т.к они еще не пересеклись друг с другом.
28-11-2016 22:03:26
Алиса
Дмитрий Довольно просто. Мы берем и от этого числа отнимаем это же число, помноженное на p/100, где p – процент.
28-11-2016 22:02:27
Алиса
Влада Ну почему же странное? Цена на пальто упала на 10%, т.е. стало составлять 90/100
часть от своей старой цены. Чтобы узнать это новую цену мы отнимает от цены это
скидку в 10%.
28-11-2016 22:02:06
Алиса
Дмитрий Потому что, нам нужно скомпенсировать то, что велосипедист выехал на 1.5 часа
позже.
28-11-2016 22:01:07
Алиса
Влада Да, конечно. Гляди: если пешеход идет x часов со скоростью 4.5 км/ч, то он пройдет
расстояние 4.5x км. Аналогично для велосипедиста. Но! Они же встретились. Значит
существует время x, в которое пешеход встретит велосипедиста.
28-11-2016 22:00:47
Алиса
Дмитрий Мы привели подобные и перенесли все неизвестные влево, а все свободные члены
вправо.
28-11-2016 21:59:32
Алиса
Влада Потому что, при умножении времени на скорость движения мы получаем пройденное
расстояние. Что в первом, что во втором произведениях. Но по условию задачи проплыл
одинаковое расстояние по течению реки и против течения, а значит, мы можем это
приравнять.
28-11-2016 21:59:12
Алиса
Дмитрий Все множители с нашей переменной x мы собираем в левой части, а свободные члены
в правой.
28-11-2016 21:57:56
Алиса
Влада 3.2 – это время, (x – 3.5) – это скорость. При их перемножении получится расстояние,
пройденное телом (из формулы скорости v = s/t, а значит s = v * t)
28-11-2016 21:57:36
Екатерина
Лолита x/15 – это нормальная скорость машин в день. Рабочие же, по условию задачи,
ежедневно выпускали по 2 машины сверх плана. Вот мы и отнимает эти две машины в
день.
28-11-2016 21:53:55
Екатерина
Ольга Умножением обеих частей равенства на 13, чтобы избавится от знаменателя.
28-11-2016 21:53:33
Екатерина
Лолита Все просто. Если x – это некоторое четное число, то n-ое следующее за ним четное = x + 2n
28-11-2016 21:50:25
Екатерина
Ольга Все просто, мы поделили обе части уравнения на множитель перед скобкой.
2*(x + x + 2 + 2 + 2) = 36 | делим обе части на 2
2/2 *(x + x + 2 + 2 + 2) = 36/2
x + x + 2 + 2 + 2 = 18;
28-11-2016 21:50:02
Екатерина
Лолита Да, при правильных действиях, ответ должен остаться верным.
28-11-2016 21:48:52
Екатерина
Ольга Если x – само по себе нечетное, то x+1 – четное, x + 2 – нечетное, x + 2 + 1 – снова
четное, а x + 2 + 2 – опять нечетное. Запись ((x + 2) + 2) вполне можно сразу
преобразовать к виду (x + 4)
28-11-2016 21:48:23
Екатерина
Лолита Мы составили его исходя из того, что x лет назад, возраст матери и удвоенный возраст
дочери должен совпадать. А значит, мы можем его приравнять друг другу.
28-11-2016 21:47:01
Екатерина
Ольга Собираем подобные члены. Те, что с переменной собираем слева, те, что без,
переносим в правую часть равенства.
28-11-2016 21:46:40
Екатерина
О, теперь понятно, а я мог после прибавления 8ки сразу поделить на 2, не оставляя это
дробью?
28-11-2016 21:45:14
Sh Polina
30-11-2016 18:46:44
0
Проведем CH ⊥ AB и DH.
DC ⊥ СН и CH ⊥ AB =>DH ⊥ AB
Из ∆ABC CH = m * sin φ.
В ∆DCH: DH = √(DC^2 + CH^2) = √(n^2 + m^2 * sin^2 φ)
Ответ: √(n^2 + m^2 * sin^2 φ)
Новость часа

Форма обратной связи