Ольга «Если его умножить на 4, к произведению прибавить 8 и полученную сумму разделить
на 2, то получится 10». Обозначим за x число. Умножим на 4 ; 4x. Прибавим 8 ; 4x + 8.
Полученную сумму поделим на 2; (4x + 8)/2. И все это теперь равно 10 ; (4x + 8)/2 = 10
Задание
Развернуть задание
Через вершину B ромба ABCD проведена прямая BM, перпендикулярная к его плоскости. Найдите расстояние от точки M до прямых, содержащих стороны ромба, если AB = 25 см, ∠BAC = 60˚, BM = 12.5 см
Развернуть задание
Новое решение
Решение
Дано: ABCD – ромб; BM ⊥ ABCD; AB = 25 см; ∠BAD = 60˚; BM = 12.5 см
MB ⊥ пл. ABCD => MB ⊥ AB и MB ⊥ BC => p(M, AB) = p(M, BC) = MB = 12.5
Проведем в плоскости ABCD отрезки BB1 ⊥ AD, BB2 ⊥ CD.
По т. о 3х перпендикулярах MB1 ⊥ AD и MB2 ⊥ DC.
MB1 = p(M, AD), MB2 = p(M, DC)
∠A = ∠C, AB = BC, поэтому ∆AB1B = ∆CB2B
BB1 = BB2 = 25 * sin 60˚ = 25 *√3/2 = 12.5√3 см
MB ⊥ пл. ABCD => MB ⊥ AB и MB ⊥ BC => p(M, AB) = p(M, BC) = MB = 12.5
Проведем в плоскости ABCD отрезки BB1 ⊥ AD, BB2 ⊥ CD.
По т. о 3х перпендикулярах MB1 ⊥ AD и MB2 ⊥ DC.
MB1 = p(M, AD), MB2 = p(M, DC)
∠A = ∠C, AB = BC, поэтому ∆AB1B = ∆CB2B
BB1 = BB2 = 25 * sin 60˚ = 25 *√3/2 = 12.5√3 см
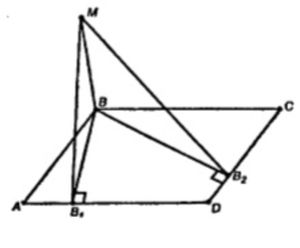
MB2 и MB1 – наклонные, их проекции (BB1 и BB2) равны => MB1 = MB2
MB1 = √(MB^2 + B1B^2) = √(12.5^2 *(1 + (√3)^2)) = 25 см
Ответ: 12.5 см, 12.5 см, 25 см, 25 см
MB1 = √(MB^2 + B1B^2) = √(12.5^2 *(1 + (√3)^2)) = 25 см
Ответ: 12.5 см, 12.5 см, 25 см, 25 см
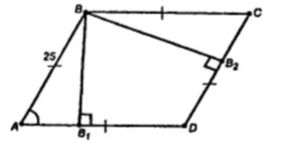
Дано: ABCD – ромб; BM ⊥ ABCD; AB = 25 см; ∠BAD = 60˚; BM = 12.5 см
MB ⊥ пл. ABCD => MB ⊥ AB и MB ⊥ BC => p(M, AB) = p(M, BC) = MB = 12.5
Проведем в плоскости ABCD отрезки BB1 ⊥ AD, BB2 ⊥ CD.
По т. о 3х перпендикулярах MB1 ⊥ AD и MB2 ⊥ DC.
MB1 = p(M, AD), MB2 = p(M, DC)
∠A = ∠C, AB = BC, поэтому ∆AB1B = ∆CB2B
BB1 = BB2 = 25 * sin 60˚ = 25 *√3/2 = 12.5√3 см
MB ⊥ пл. ABCD => MB ⊥ AB и MB ⊥ BC => p(M, AB) = p(M, BC) = MB = 12.5
Проведем в плоскости ABCD отрезки BB1 ⊥ AD, BB2 ⊥ CD.
По т. о 3х перпендикулярах MB1 ⊥ AD и MB2 ⊥ DC.
MB1 = p(M, AD), MB2 = p(M, DC)
∠A = ∠C, AB = BC, поэтому ∆AB1B = ∆CB2B
BB1 = BB2 = 25 * sin 60˚ = 25 *√3/2 = 12.5√3 см
MB2 и MB1 – наклонные, их проекции (BB1 и BB2) равны => MB1 = MB2
MB1 = √(MB^2 + B1B^2) = √(12.5^2 *(1 + (√3)^2)) = 25 см
Ответ: 12.5 см, 12.5 см, 25 см, 25 см
MB1 = √(MB^2 + B1B^2) = √(12.5^2 *(1 + (√3)^2)) = 25 см
Ответ: 12.5 см, 12.5 см, 25 см, 25 см