Ольга «Если его умножить на 4, к произведению прибавить 8 и полученную сумму разделить
на 2, то получится 10». Обозначим за x число. Умножим на 4 ; 4x. Прибавим 8 ; 4x + 8.
Полученную сумму поделим на 2; (4x + 8)/2. И все это теперь равно 10 ; (4x + 8)/2 = 10
Задание
Развернуть задание
Даны два двугранных угла, у которых одна грань общая, а две другие грани являются различными полуплоскостями одной плоскости. Докажите, что сумма этих двугранных углов равна 180˚.
Развернуть задание
Новое решение
Решение
Пусть α и β пересекаются по AB. Выберем произвольную точку O ∈ AB. В плоскости α проведем прямую CD через O так, чтобы CD ⊥ AB.
В плоскости β проведем луч OF так, чтобы OF ⊥ AB.
Двугранному углу DABF соответствует линейный угол FOD; двугранному CABF соответствует линейный угол FOC.
Углы FOD и FOC – смежные, ∠FOD + ∠FOC = 180˚.
В плоскости β проведем луч OF так, чтобы OF ⊥ AB.
Двугранному углу DABF соответствует линейный угол FOD; двугранному CABF соответствует линейный угол FOC.
Углы FOD и FOC – смежные, ∠FOD + ∠FOC = 180˚.
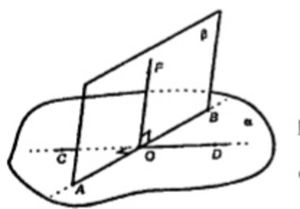
Пусть α и β пересекаются по AB. Выберем произвольную точку O ∈ AB. В плоскости α проведем прямую CD через O так, чтобы CD ⊥ AB.
В плоскости β проведем луч OF так, чтобы OF ⊥ AB.
Двугранному углу DABF соответствует линейный угол FOD; двугранному CABF соответствует линейный угол FOC.
Углы FOD и FOC – смежные, ∠FOD + ∠FOC = 180˚.
В плоскости β проведем луч OF так, чтобы OF ⊥ AB.
Двугранному углу DABF соответствует линейный угол FOD; двугранному CABF соответствует линейный угол FOC.
Углы FOD и FOC – смежные, ∠FOD + ∠FOC = 180˚.