Ольга «Если его умножить на 4, к произведению прибавить 8 и полученную сумму разделить
на 2, то получится 10». Обозначим за x число. Умножим на 4 ; 4x. Прибавим 8 ; 4x + 8.
Полученную сумму поделим на 2; (4x + 8)/2. И все это теперь равно 10 ; (4x + 8)/2 = 10
Задание
Развернуть задание
Из вершины B треугольника ABC, сторона AC которого лежит в плоскости α, проведен к этой плоскости перпендикуляр BB1. Найдите расстояния от точки B до прямой AC и до плоскости α, если AB = 2 см, ∠BAC = 150˚ и двугранный угол BACB1 = 45˚.
Развернуть задание
Новое решение
Решение
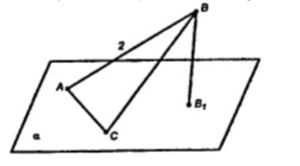
Проведем BD ⊥ AC. По т. о 3х перпендикулярах BD ⊥ AC.
∠BAC = 150˚
p(B, AC) = BD.
∠BAD = 180˚ - 150˚ = 30˚.
BD = AB/2 = 1/2 * 2 = 1 см
По условию ∠B1DB = 45˚, так как B1DB – линейный угол двугранного угла BACB1.
p(B, α) = BB1 = DB * sin 45˚ = √2/2 см
Ответ: p(B, AC) = 1см, p(B, α) = √2/2 см
∠BAC = 150˚
p(B, AC) = BD.
∠BAD = 180˚ - 150˚ = 30˚.
BD = AB/2 = 1/2 * 2 = 1 см
По условию ∠B1DB = 45˚, так как B1DB – линейный угол двугранного угла BACB1.
p(B, α) = BB1 = DB * sin 45˚ = √2/2 см
Ответ: p(B, AC) = 1см, p(B, α) = √2/2 см
