Задание
Развернуть задание
Докажите, что если все ребра тетраэдра равны, то все его двугранные углы также равны.
Найдите эти углы.
Найдите эти углы.
Развернуть задание
Новое решение
Решение
Построим SO ⊥ ABC.
SA, SB, SC – наклонные, а равные наклонные имеют равные проекции =>AO = BO = CO;
Поэтому в плоскости ABC AO = R, R – радиус описанной окружности.
∆ABC – правильный; продолжим AO, CO и BO до пересечения их со сторонами треугольника. BB1 ⊥ AC, CC1 ⊥ AB1, AA1 ⊥ BC.
∆OB1S = ∆OC1S = ∆OA1S – по двум катетам, ∠SB1O = ∠SC1O = ∠SA1O (из равенства треугольников)
Раз все ребра тетраэдра равны, то все двугранные углы равны.
Найдем ∠SA1O.
Пусть a – ребро тетраэдра.
∆BSC: SA1 = a * sin 60˚ = a * √3/2 = a*√3/2
∆ABC: OA1 = 1/3AA1 = 1/3 * a √3/2 = a/(2√3)
∆SA1O: cos φ = OA1/SA1 = a/(2√3) : a*√3/2 = 1/3
φ – острый угол => φ = arccos 1/3
Ответ: φ = arccos 1/3
SA, SB, SC – наклонные, а равные наклонные имеют равные проекции =>AO = BO = CO;
Поэтому в плоскости ABC AO = R, R – радиус описанной окружности.
∆ABC – правильный; продолжим AO, CO и BO до пересечения их со сторонами треугольника. BB1 ⊥ AC, CC1 ⊥ AB1, AA1 ⊥ BC.
∆OB1S = ∆OC1S = ∆OA1S – по двум катетам, ∠SB1O = ∠SC1O = ∠SA1O (из равенства треугольников)
Раз все ребра тетраэдра равны, то все двугранные углы равны.
Найдем ∠SA1O.
Пусть a – ребро тетраэдра.
∆BSC: SA1 = a * sin 60˚ = a * √3/2 = a*√3/2
∆ABC: OA1 = 1/3AA1 = 1/3 * a √3/2 = a/(2√3)
∆SA1O: cos φ = OA1/SA1 = a/(2√3) : a*√3/2 = 1/3
φ – острый угол => φ = arccos 1/3
Ответ: φ = arccos 1/3
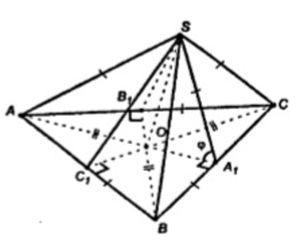
Построим SO ⊥ ABC.
SA, SB, SC – наклонные, а равные наклонные имеют равные проекции =>AO = BO = CO;
Поэтому в плоскости ABC AO = R, R – радиус описанной окружности.
∆ABC – правильный; продолжим AO, CO и BO до пересечения их со сторонами треугольника. BB1 ⊥ AC, CC1 ⊥ AB1, AA1 ⊥ BC.
∆OB1S = ∆OC1S = ∆OA1S – по двум катетам, ∠SB1O = ∠SC1O = ∠SA1O (из равенства треугольников)
Раз все ребра тетраэдра равны, то все двугранные углы равны.
Найдем ∠SA1O.
Пусть a – ребро тетраэдра.
∆BSC: SA1 = a * sin 60˚ = a * √3/2 = a*√3/2
∆ABC: OA1 = 1/3AA1 = 1/3 * a √3/2 = a/(2√3)
∆SA1O: cos φ = OA1/SA1 = a/(2√3) : a*√3/2 = 1/3
φ – острый угол => φ = arccos 1/3
Ответ: φ = arccos 1/3
SA, SB, SC – наклонные, а равные наклонные имеют равные проекции =>AO = BO = CO;
Поэтому в плоскости ABC AO = R, R – радиус описанной окружности.
∆ABC – правильный; продолжим AO, CO и BO до пересечения их со сторонами треугольника. BB1 ⊥ AC, CC1 ⊥ AB1, AA1 ⊥ BC.
∆OB1S = ∆OC1S = ∆OA1S – по двум катетам, ∠SB1O = ∠SC1O = ∠SA1O (из равенства треугольников)
Раз все ребра тетраэдра равны, то все двугранные углы равны.
Найдем ∠SA1O.
Пусть a – ребро тетраэдра.
∆BSC: SA1 = a * sin 60˚ = a * √3/2 = a*√3/2
∆ABC: OA1 = 1/3AA1 = 1/3 * a √3/2 = a/(2√3)
∆SA1O: cos φ = OA1/SA1 = a/(2√3) : a*√3/2 = 1/3
φ – острый угол => φ = arccos 1/3
Ответ: φ = arccos 1/3
